Tích phân Riemann và định lý Fubini¶
1. Định lý Fubini¶
Trong giải tích hàm nhiều biến, định lý Fubini là một công cụ không thể thiếu để giúp cho việc tính tích phân kép trở nên dễ dàng hơn. Định lý Fubini được phát biểu như sau:
Cho \(f(x,y) \geq 0, \forall(x,y) \in \mathcal{D} = \{(x,y) \in \mathbb{R}^2 : a \leq x \leq b, c \leq y \leq d\}\) là hàm liên tục trên miền \(\mathcal{D}\). Khi đó $\(\iint\limits_D f(x,y)dxdy = \int\limits_a^b \left [ \int\limits_c^df(x,y)dy\right ]dx = \int\limits_c^d \left [ \int\limits_a^bf(x,y)dx\right ]dy\)$
Chú ý: Trong trường hợp đặc biệt nếu \(f(x,y) = f_1(x)f_2(y)\) thì $\(\iint\limits_D f(x,y)dxdy = \int\limits_a^b \left [ \int\limits_b^df_1(x)f_2(y)dy\right ]dx = \\ \int\limits_a^b f_1(x) \left [ \int\limits_b^df_2(y)dy\right ]dx = \int\limits_a^b f_1(x)dx \int\limits_b^df_2(y)dy\)$
Ví dụ: Tính tích phân \(I = \iint\limits_D(3y^2-x)dxdy\), với \(\mathcal{D} = \{(x,y) : 0 \leq x \leq 2, 1 \leq y \leq 2\}\)
Giải: Theo định lý Fubini, đầu tiên lấy tích phân theo biến \(y\), ta có: $\(I = \iint\limits_D (3y^2 - x)dxdy = \int\limits_0^2 \left [ \int\limits_1^2 (3y^2 - x)dy\right ]dx = \int\limits_0^2 \left [ y^3 - xy\right ]_{y=1}^{y=2}dx \\ = \int\limits_0^2 \left [ (8-2x)-(1-x) \right ]dx = \int\limits_0^2 (7-x)dx = \left [ 7x - \frac{x^2}{2} \right ]_0^2 = 12\)$
Bài tập: Tính tích phân trong ví dụ bằng cách lấy tích phân theo biến \(x\) đầu tiên.
2. Tích phân Riemann¶
Ta đều biết ứng dụng thường dùng nhất của tích phân là để tính diện tích. Trong phần này, ta sẽ cùng đi qua một phương pháp dùng diện tích để tính gần đúng giá trị của tích phân, gọi là tổng Riemann. Phương pháp này cực kì hữu hiệu khi ta cần tính tích phân mà không biết chính xác hàm \(f(x)\), chỉ biết tập hợp gồm toạ độ các điểm \(x\) và \(f(x)\) trong một miền xác định.
Cho hàm số \(f(x)\) xác định trên đoạn \([a,b]\) \((a<b)\). Chia đoạn \([a,b]\) thành \(n\) phần nhỏ hữu hạn \([x_{i-1}, x_i]\), \((i=1,\dots,n)\) bởi những điểm $\(a=x_0<x_1<x_2<\ldots<x_{i-1}<x_i<\ldots<x_n=b\)$
Trên mỗi phần nhỏ này \([x_{i-1}, x_i]\) chọn bất kỳ một điểm \(\xi_i \in [x_{i-1}, x_i]\) và thành lập tổng \(\sigma = \sum\limits_{i=1}^n f(\xi_i)\Delta x_i\), với \(\Delta x_i = x_i - x_{i-1}>0\).
Tổng \(\sigma = \sum\limits_{i=1}^n f(\xi_i)\Delta x_i\) được gọi là tổng tích phân của hàm số \(f(x)\) trên đoạn \([a,b]\), hay tổng Riemann. Nói cách khác, tổng Riemann là tổng diện tích của các hình chữ nhật có bề ngang \(\Delta x_i\) và chiều cao \(f(\xi_i)\) trên miền \([a,b]\). Ta có thể dùng tổng Riemann để xấp xỉ giá trị của tích phân \(\int\limits_a^b f(x)dx\).

Hình 1: Tổng Riemann cho hàm số \(f(x) = x^2\) trong khoảng \([-4,4]\) được chia thành 20 đoạn nhỏ, hay bước chia \(\Delta x_i = 0.2\) và \(\xi_i = (x_i + x_{i-1})/2\).
Số hữu hạn \(I\in \mathbb{R}\) được gọi là giới hạn của tổng tích phân \(\sigma\) khi \(\lambda \to 0\), \((\lambda = \max\{\Delta x_i, i=1,\dots,n\})\), nếu như với mọi \(\varepsilon>0\), \(\exists \delta=\delta(\varepsilon)>0\) sao cho đoạn \([a,b]\) bị chia thành những đoạn nhỏ với độ dài \(\Delta x_i<\delta\), có nghĩa là \(\lambda<\delta\), luôn có bất đẳng thức \(\left |\sigma - I \right | < \varepsilon\) không phụ thuộc vào cách chia đoạn \([a,b]\) thành những đoạn nhỏ và cách chọn điểm \(\xi_i\) trên những đoạn nhỏ \([x_{i-1}, x_i]\). Lúc này ta viết $\(\lim\limits_{\lambda \to 0} \sigma = I\)$
Nếu tổng tích phân \(\sigma\) có giới hạn hữu hạn khi \(\lambda \to 0\), có nghĩa là \(\lim\limits_{\lambda \to 0} \sigma = I\) thì \(I\) là tích phân xác định của hàm số \(f(x)\) trong khoảng \([a,b]\). Trong trường hợp này những số \(a\) và \(b\) trở thành cận trên và cận dưới của tích phân.
Như vậy ta có tích phân Riemann $\(\int\limits_a^b f(x)dx = I = \lim\limits_{\lambda \to 0}\sigma = \lim\limits_{\lambda \to 0} \sum\limits_{i=1}^n f(\xi_i)\Delta x_i\)$
2.1. Các dạng của tổng Riemann¶
Dựa vào cách chọn \(\xi_i\) mà ta có thể chia tổng Riemann ra làm 3 dạng chính:
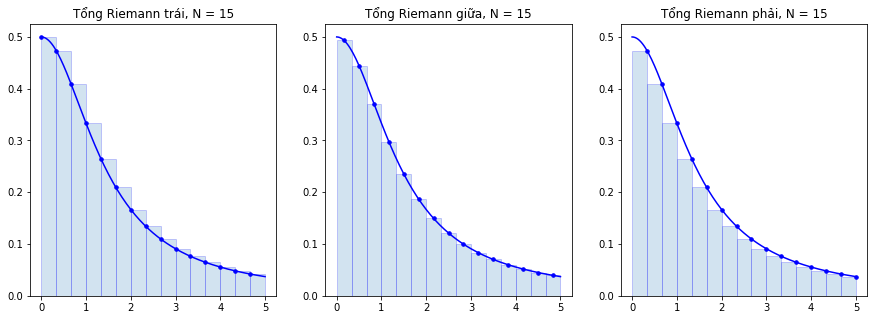
Tổng Riemann trái khi \(\xi_i = x_{i-1}\).
Tổng Riemann giữa khi \(\xi_i = (x_{i-1} + x_i)/2\).
Tổng Riemann phải khi \(\xi_i = x_i\).
Ngoài ra, còn một phương pháp tương tự tổng Riemann được gọi là quy tắc hình thang. Thay vì sử dụng \(f(\xi_i)\), ta thay bằng trung bình cộng của \(f(x_{i-1})\) và \(f(x_i)\). Khi đó ta có $\(I = \int\limits_a^b f(x)dx \approx \sum\limits_{i=1}^n \frac{f(x_{i-1})-f(x_i)}{2} \Delta x_i\)$
Tổng \(\sum\limits_{i=1}^n \frac{f(x_{i-1})-f(x_i)}{2} \Delta x_i\) chính là tổng diện tích các hình thang có độ dài cạnh bên là \(\Delta x_i\) và độ dài hai đáy lần lượt là \(f(x_{i-1})\) và \(f(x_i)\).
Ví dụ: Với hàm \(f(x) = \frac{1}{2+x^2}\) trong khoảng \([0,5]\), ta vẽ được ba dạng chính của tổng Riemann.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
f = lambda x : 1/(2+x**2)
a = 0; b = 5; N = 15
x = np.linspace(a,b,N+1)
y = f(x)
X = np.linspace(a,b,10*N+1)
Y = f(X)
plt.figure(figsize=(15,5))
plt.subplot(1,3,1)
plt.plot(X,Y,'b')
x_left = x[:-1] # Điểm bên trái
y_left = y[:-1]
plt.plot(x_left,y_left,'b.',markersize=7)
plt.bar(x_left,y_left,width=(b-a)/N,alpha=0.2,align='edge', edgecolor='b')
plt.title('Tổng Riemann trái, N = {}'.format(N))
plt.subplot(1,3,2)
plt.plot(X,Y,'b')
x_mid = (x[:-1] + x[1:])/2 # Điểm giữa
y_mid = f(x_mid)
plt.plot(x_mid,y_mid,'b.',markersize=7)
plt.bar(x_mid,y_mid,width=(b-a)/N,alpha=0.2, edgecolor='b')
plt.title('Tổng Riemann giữa, N = {}'.format(N))
plt.subplot(1,3,3)
plt.plot(X,Y,'b')
x_right = x[1:] # Điểm bên phải
y_right = y[1:]
plt.plot(x_right,y_right,'b.',markersize=7)
plt.bar(x_right,y_right,width=-(b-a)/N,alpha=0.2,align='edge', edgecolor='b')
plt.title('Tổng Riemann phải, N = {}'.format(N))
plt.show()
2.2. Dùng tổng Riemann để tính gần đúng tích phân xác định¶
Xét ví dụ phía trên. Ta có thể tính được giá trị chính xác của \(\int\limits_0^5 \frac{1}{2+x^2} dx \approx 0.9158\) bằng hàm quad trong thư viện scipy.
import scipy.integrate as integrate
I, err = integrate.quad(lambda x : 1/(2+x**2), 0, 5)
I
0.9158118420285284
Bây giờ ta tính gần đúng giá trị của tích phân theo tổng Riemann trái, giữa và phải với \(N=15\) đoạn nhỏ.
dx = (b-a)/N
x_trai = np.linspace(a,b-dx,N)
x_giua = np.linspace(dx/2,b - dx/2,N)
x_phai = np.linspace(dx,b,N)
rsum_trai = np.sum(f(x_trai) * dx)
print("Tổng Riemann trái:",rsum_trai)
print("Sai số của tổng Riemann trái:",np.abs(rsum_trai - I),"\n")
rsum_giua = np.sum(f(x_giua) * dx)
print("Tổng Riemann giữa:",rsum_giua)
print("Sai số của tổng Riemann giữa:",np.abs(rsum_giua - I),"\n")
rsum_phai = np.sum(f(x_phai) * dx)
print("Tổng Riemann phải:",rsum_phai)
print("Sai số của tổng Riemann phải:",np.abs(rsum_phai - I))
Tổng Riemann trái: 0.9928454115593366
Sai số của tổng Riemann trái: 0.0770335695308082
Tổng Riemann giữa: 0.9158752708708305
Sai số của tổng Riemann giữa: 6.342884230214896e-05
Tổng Riemann phải: 0.8385244239050156
Sai số của tổng Riemann phải: 0.07728741812351281
Ta có thể thấy sai số của phép tổng Riemann giữa là nhỏ nhất, hay nói cách khác, tổng Riemann giữa có thể được dùng để xấp xỉ gần đúng nhất giá trị tích phân trong hầu hết các trường hợp.
Tăng \(N\) lên thành \(1000000\), khi đó giá trị xấp xỉ của tổng Riemann tiến rất gần đến giá trị chính xác của \(I\), sai số giảm xuống rất nhỏ và trở nên không đáng kể.
dx = (b-a)/1000000
x_trai = np.linspace(a,b-dx,1000000)
x_giua = np.linspace(dx/2,b - dx/2,1000000)
x_phai = np.linspace(dx,b,1000000)
rsum_trai = np.sum(f(x_trai) * dx)
print("Tổng Riemann trái:",rsum_trai)
print("Sai số của tổng Riemann trái:",np.abs(rsum_trai - I),"\n")
rsum_giua = np.sum(f(x_giua) * dx)
print("Tổng Riemann giữa:",rsum_giua)
print("Sai số của tổng Riemann giữa:",np.abs(rsum_giua - I),"\n")
rsum_phai = np.sum(f(x_phai) * dx)
print("Tổng Riemann phải:",rsum_phai)
print("Sai số của tổng Riemann phải:",np.abs(rsum_phai - I))
Tổng Riemann trái: 0.915812999435907
Sai số của tổng Riemann trái: 1.1574073786047023e-06
Tổng Riemann giữa: 0.9158118420285429
Sai số của tổng Riemann giữa: 1.454392162258955e-14
Tổng Riemann phải: 0.9158106846210925
Sai số của tổng Riemann phải: 1.1574074358922104e-06
2.3. Hàm sai số của tổng Riemann¶
Vừa rồi ta đã tính được sai số của tổng Riemann so với giá trị chính xác của tích phân. Nhưng trong thực tế, ta sử dụng tổng Riemann khi không biết hàm \(f(x)\) là gì, cũng như giá trị chính xác của tích phân \(\int\limits_a^bf(x)dx\) là bao nhiêu. Vậy có cách nào để tính được sai số của phép tổng Riemann theo số khoảng chia \(N\) được không? Hay ta cần tăng \(N\) đến bao nhiêu để giá trị xấp xỉ có thể chấp nhận được?
Gọi \(M_1 = \max |f'(x)|\) và \(M_2 = \max |f''(x)|\) trong khoảng \([a,b]\).
Khi đó:
Sai số của tổng Riemann trái $\( \left | \int\limits_a^b f(x)dx - \sum\limits_{i=1}^n f(x_{i-1})\Delta x_i \right | \leq \frac{(b-a)^2}{2N}M_1\)$
Sai số của tổng Riemann phải $\( \left | \int\limits_a^b f(x)dx - \sum\limits_{i=1}^n f(x_i)\Delta x_i \right | \leq \frac{(b-a)^2}{2N}M_1\)$
Sai số của tổng Riemann giữa $\( \left | \int\limits_a^b f(x)dx - \sum\limits_{i=1}^n f\left (\frac{x_{i-1}+x_i}{2} \right)\Delta x_i \right | \leq \frac{(b-a)^3}{24N^2}M_2\)$
Bên cạnh đó, ta cũng có sai số công thức hình thang $\( \left | \int\limits_a^b f(x)dx - \sum\limits_{i=1}^n \frac{f(x_{i-1})-f(x_i)}{2} \Delta x_i \right | \leq \frac{(b-a)^3}{12N^2}M_2\)$
Nhận xét: Từ 4 công thức sai số trên, ta có thể thấy công thức hình thang và tổng Riemann giữa có thể xấp xỉ giá trị tích phân tốt hơn khi \(N\to\infty\), do 2 công thức này tỉ lệ nghịch với \(N^2\), trong khi sai số của tổng Riemann trái và phải chỉ tỉ lệ nghịch với \(N\).
3. Bài tập¶
Thành lập 1 hàm Python để tính gần đúng tích phân bằng tổng Riemann, với \(5\) tham số đầu vào \(f\), \(a\), \(b\), \(N\) và \(m\). Trong đó:
\(f\) là hàm trong dấu tích phân.
\([a,b]\) là miền giá trị.
\(N\) là số đoạn chia.
\(m\) là dạng của tổng Riemann (trái, phải, hoặc giữa).
Tìm số đoạn chia \(N\) để sai số của tổng Riemann giữa của hàm \(f(x)=\frac{1}{x}\) trên đoạn \([0,1]\) không vượt quá \(10^{-6}\).
Hệ số lực nâng \(c_l\) đối với một biên dạng cánh máy bay được tính bằng cách tích phân hệ số áp suất \(C_p\) (bỏ qua ma sát) trên toàn bộ bề mặt cánh. File Excel NACA 2412_Cp_alpha5.xlsx chứa toạ độ các điểm \(x\), \(y\) của một biên dạng cánh máy bay NACA 2412 ở góc tấn \(\alpha=5^{\circ}\) và hệ số áp suất tại từng điểm. Tính xấp xỉ lực nâng đối với biên dạng cánh máy bay này bằng phương pháp tổng Riemann, biết
\(c_l = \cos(\alpha)\int\limits_0^1(C_{p,l}-C_{p,u})dx - \sin(\alpha)\int\limits_0^1 \left (C_{p,u}\frac{dy_u}{dx}-C_{p,l}\frac{dy_l}{dx} \right )dx\)
\(C_{p,u}\) là hệ số lực nâng của mặt trên \((y>0)\) và \(C_{p,l}\) là hệ số lực nâng của mặt dưới \((y<0)\).
Giá trị chính xác của \(c_l \approx 0.8579\).
4. Tài liệu tham khảo¶
[1] Nguyễn Đình Huy. (2018). Giáo trình Giải tích 1, TP. HCM: NXB Đại học quốc gia TP. HCM.
[2] Nguyễn Đình Huy. (2018). Giáo trình Giải tích 2, TP. HCM: NXB Đại học quốc gia TP. HCM.
[3] https://www.math.ubc.ca/~pwalls/math-python/integration/riemann-sums/
[4] https://en.wikipedia.org/wiki/Riemann_sum
