Lý thuyết thông tin¶

Đóng góp: Ngô Hoàng Anh, École Polytechnique, Institut Polytechnique de Paris, Cộng hoà Pháp

Lý thuyết thông tin nghiên cứu về đo đạc lượng, lưu trữ và truyền dẫn thông tin. Khái niệm về lý thuyết thông tin cũng như nền móng của lĩnh vực này được xây dựng bởi công trình của Harry Nyquist và Ralph Hartley vào những năm 1920, và sau này là Claude Shannon vào những năm 1940.

Lý thuyết này là “nút giao” của nhiều lĩnh vực khác nhau như xác suất thống kê, khoa học máy tính, cơ học thống kê, kĩ thuật thông tin và kĩ thuật điện, dùng để xác định giới hạn cơ bản trong các hoạt động xử lý dữ liệu. Ứng dụng của nó đã rất phong phú ngay từ những ngày đầu tiên, ví dụ như xử lý ngôn ngữ tự nhiên, mật mã học, mạng lưới thần kinh, sự tiến hoá và chức năng của các mã phân tử, sinh thái học, vật lý nhiệt, máy tính lượng tử và rất nhiều những hình thức phân tích dữ liệu khác.

Những ứng dụng thực tiễn cơ bản của lý thuyết thông tin bao gồm: nén không mất dữ liệu (ZIP), nét mất dữ liệu (MP3, JPG), hay mã hoá kênh (DSL).

Đầu tiên, chúng ta quy ước

$\mathcal{X}$ là tập hợp tất cả các phần tử $\{x_1, x_2, ..., x_n\}$ mà biến ngẫu nhiên $X$ có thể nhận giá trị;
$\mathcal{Y}$ là tập hợp tất cả các phần tử $\{y_1, y_2, ..., y_n\}$ mà biến ngẫu nhiên $Y$ có thể nhận giá trị;
$p(x)$, $p(y)$ lần lượt là xác suất tại các giá trị $x$ và $y$.

1. Sơ lược về thông tin và lượng tin¶

Đối tượng nghiên cứu chính của lý thuyết thông tin chính là “thông tin”. Thông tin này có thể được mã hoá bằng bất kì điều gì, với một hay nhiều định dạng khác nhau. Như vậy, làm cách nào để định lượng thông tin?

Trong bài báo kinh điển của mình vào năm 1948, Claude Shannon đã lần đầu giới thiệu thuật ngữ “bit” để làm đơn vị đo lường thông tin, mà đơn vị này ban đầu cũng đã được đề xuất bởi John Tukey. Lý do “bit” được sử dụng đơn giản là vì các máy thu phát tín hiệu, hay kể cả các hệ thống máy tính hiện đại mà chúng ta làm việc ngày nay, bất kì thông tin nào đều được mã hoá bởi một chuỗi nhị phân các số $0$ và $1$. Như vậy, một chuỗi nhị phân độ dài $n$ sẽ có $n$ bit thông tin.

Để “lượng hoá” lượng thông tin này thành số lượng bit, Shannon đề xuất một hàm “lượng tin”, hay sẽ chủ yếu đề cập đến với tên entropy, nhằm tính toán số “bit” thông tin nhận được ứng với một (nhóm) sự kiện $X$ nào đó.

\[ I(X) = -\log_2 p(X) \]

Lấy ví dụ đơn giản, giả sử chúng ta có một mã là một chuỗi nhị phân độ dài 5, chẳng hạn như “10001”. Khi đó, lượng tin của mã này sẽ là

\[ I("10001") = -\log_2 p("10001") = -\log_2 \frac{1}{2^5} = -(-5) = 5 (\text{bits}) \]

2. Entropy¶

Như đã đề cập ở trên, lý thuyết thông tin được xây dựng dựa trên nền tảng xác suất thống kê. Thông số quan trọng nhất của thông tin là entropy (lượng thông tin chứa trong một biến ngẫu nhiên). Từ entropy, các khái niệm entropy hợp hay entropy có điều kiện cũng được hình thành để đo lường thông tin tương hỗ (lượng thông tin chung giữa hai biến ngẫu nhiên).

Entropy của biến $X$, $H(X)$, được tính bằng

\[ H(X) = \mathbf{E}[I(x)] = - \sum_{x \in \mathcal{X}} p(x) \log p(x) \]

Một trong những trường hợp thường gặp nhất của entropy cho biến ngẫu nhiên là hàm entropy nhị phân .tức là entropy cho biến ngẫu nhiên $X$ có phân phối xác suất $p(x)$ với duy nhất hai khả năng $\{0, 1\}$.

\[ H_{\mathbb{b}} (X) = \sum_{x \in \mathcal{X}} - p(x) \log p(x) - (1-p(x)) \log (1-p(x)) \]

Trong trường hợp $X$ là một biến ngẫu nhiên liên tục, entropy của $X$ sẽ được tính theo công thức tích phân:

\[ H(X) = - \int_{x \in \mathcal{X}} p(x) \log p(x) dx \]

Từ công thức biểu diễn, chúng ta có thể rút ra một số tính chất cơ bản của entropy như sau

Entropy có giá trị không âm, tức là $H(X) \geq 0, \quad \forall X$.
$X$ sẽ chứa lượng thông tin cực đại, hay $H(X)$ đạt giá trị lớn nhất, nếu như mọi phần tử trong tập các biến cố khả dĩ có chứa lượng thông tin như nhau. Điều này có nghĩa là $$ H(X) \leq \log(n), $$ với dấu $“=”$ xảy ra khi và chỉ khi $p_{x_1} = p_{x_2} = … = p_{x_n} = \frac{1}{n}$.

3. Thông tin tương hỗ¶

Entropy đã cung cấp cho chúng ta định lượng thông tin của một biễn ngẫu nhiên duy nhất; tuy nhiên, chuyện gì sẽ xảy ra nếu có hai biến ngẫu nhiên (rời rạc hoặc liên tục)? Những khái niệm được đề cập tới trong phần này sẽ giúp thể hiện những khía cạnh khác nhau của câu hỏi “Thông tin của cả hai biến $X$ và $Y$ sẽ như thế nào so với thông tin được chứa trong từng biến riêng lẻ? Có thông tin nào bị thừa, thiếu, hay đều phân biệt và độc nhất?”

3.1. Entropy hợp (Joint Entropy)¶

Entropy hợp của hai biến ngẫu nhiên $(X, Y)$ là entropy dựa trên phân phối xác suất đồng thời (join distribution) của hai biến $(X, Y)$.

Ví dụ, nếu cặp $(X,Y)$ biểu diễn vị trí của một quân cờ trên bàn cờ vua, với $X$ là toạ độ hàng và $Y$ là toạ độ cột, khi đó, entropy hợp của toạ độ hàng và toạ độ cột của con cờ sẽ là entropy của cặp toạ độ của quân cờ.

Entropy hợp của cặp $(X,Y)$ được biểu diễn như sau

\[ H(X,Y) = \mathbf{E}_{X,Y} [- \log p(x,y)] = - \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x,y) \log p(x, y) \]

Trong trường hợp $(X,Y)$ là một cặp biến ngẫu nhiên liên tục, entropy hợp của cặp này cũng sẽ được tính tương tự như sau

\[ H(X, Y)= - \int_{\mathcal{Y}} \int_{\mathcal{X}} p(x, y) \log p(x, y) dx dy \]

3.2. Entropy có điều kiện (Conditional entropy)¶

Entropy có điều kiện, hay điều kiện không chắc chắn (conditional uncertainty), của $X$ với một biến ngẫu nhiên cho trước $Y$ (hay còn gọi là độ mờ của $X$ đối với $Y$) là giá trị kì vọng của entropy của $X$ theo phân bố của $Y$

\[\begin{split} \begin{eqnarray}H(X|Y) & = & \mathbf{E}_{Y} [H(X|y)] \\ & = & - \sum_{y \in \mathcal{Y}} p(y) \sum_{x \in \mathcal{X}} p(x|y) \log p(x|y) \\ & = & - \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x,y) \log p(x|y) \\ & = & - \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x,y)\log \frac{p(x,y)}{p(y)} \\ & = & - [\sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x,y)\log p(x,y) - \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}}{p(x, y) \log p(y)}] \\ & = & - [\sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x,y)\log p(x,y) - \sum_{y \in \mathcal{Y}}{p(y) \log p(y)}] \\ & = & H(X, Y) - H(Y) \end{eqnarray} \end{split}\]

Nếu $X, Y$ là các biến liên tục, entropy có điều kiện sẽ được tính tương tự như sau

\[\begin{split} \begin{eqnarray} H(X|Y) & = & - \int_{\mathcal{Y}} \int_{\mathcal{X}} p(x,y) \log p(x|y) dx dy \\ & = & - \int_{\mathcal{Y}} \int_{\mathcal{X}} p(x,y) \log \frac{p(x,y)}{p(y)} dx dy \\ & = & - \int_{\mathcal{Y}} \int_{\mathcal{X}} p(x,y) [\log p(x,y) - \log p(y)] dx dy \\ & = & - \int_{\mathcal{Y}} \int_{\mathcal{X}} p(x,y) \log p(x,y) dx dy + \int_{\mathcal{Y}} \int_{\mathcal{X}} p(x,y) \log p(y) dx dy \\ & = & - \int_{\mathcal{Y}} \int_{\mathcal{X}} p(x,y) \log p(x,y) dx dy + \int_{\mathcal{Y}} p(y) \log p(y) dy \\ & = & H(X, Y) - H(Y) \end{eqnarray} \end{split}\]

Như vậy cả hai trường hợp biến liên tục và biến rời rạc đều dẫn tới một kết quả quan trọng đó là:

\[ H(X|Y) = H(X,Y) - H(Y) \]

3.3. Thông tin tương hỗ (Mutual Information)¶

Từ những định nghĩa trên, chúng ta thấy:

Thông tin chứa bởi cả cặp $(X, Y)$ là $H(X,Y)$.
Thông tin chứa trong $X$ nhưng lại không chứa trong $Y$ là $H(X|Y)$.
Thông tin chứa trong $Y$ nhưng lại không nằm trong $X$ là $H(Y|X)$.

Chúng ta có thể trả lời câu hỏi sau đây: “Lượng thông tin giống nhau, tức là cùng được biết bởi cả hai biến $X$ và $Y$, là bao nhiêu?”. Một cách rất trực quan, chúng ta xây dựng khái niệm thông tin tương hỗ như sau

\[ I(X,Y) = H(X,Y) - H(X|Y) - H(Y|X) \]

Như vậy, thông tin tương hỗ là lượng thông tin thu được từ một biến ngẫu nhiên thông qua việc quan sát giá trị của một biến ngẫu nhiên khác.

\[ I(X;Y) = \mathbf{E}_{X,Y} [I(x \in \mathcal{X},y \in \mathcal{Y})] = \sum_{x \in \mathcal{X}}\sum_{y \in \mathcal{Y}} p(x,y) \log \frac{p(x,y)}{p(x) p(y)} \]

Hai công thức trên cho chúng ta một tính chất quan trọng của thông tin tương hỗ, tính đối xứng

\[ I(X;Y) = I(Y;X). \]

Ngoài ra, dựa vào mối quan hệ của entropy hợp và entropy có điều kiện, các biểu thức sau đây đều tương đương với thông tin tương hỗ

\[\begin{split}\begin{eqnarray} I(X;Y) & = & I(Y;X) \\ & = & H(X,Y) - H(X|Y) - H(Y|X) \\ & = & H(X) - H(X|Y) \\ & = & H(Y) - H(Y|X) \\ & = & H(X) + H(Y) - H(X,Y) \end{eqnarray} \end{split}\]

Từ đây, chúng ta thấy rằng thông tin tương hỗ luôn nhận giá trị không âm (tức là $H(X,Y) \geq 0$), và dấu $"="$ xảy ra khi và chỉ khi $X$ và $Y$ là hai biến ngẫu nhiên hoàn toàn độc lập. Khi đó, việc biết thông tin của một biến không cho chúng ta bất cứ thông tin gì về biến còn lại, và ngược lại.

4. Phân kì Kullback - Leibler (Kullback - Leibler divergence)¶

Nếu như norm có thể được sử dụng để đo khoảng cách giữa hai điểm trong không gian với số chiều bất kì, chúng ta cũng có thể tìm cách thực hiện tương tự với các phân phối xác suất. Để xác định hai phân phối có gần nhau hay không, phân kì Kullback - Leibler là phương pháp đo tốt nhất, sử dụng lý thuyết thông tin, để thực hiện công việc này.

Giả sử chúng ta có hai hàm mật độ/hàm khối xác suất khác nhau cho cùng một biến ngẫu nhiên $X$: một hàm “thật” $p(x)$ cho phân phối xác suất $P$ và một hàm ước lượng bất kì $q(x)$ cho phân phối xác suất $Q$. Khi đó, phân kì Kullback - Leibler (hay entropy tương đối) được tính bằng

\[ D_{KL} (p(X) || q(X)) = \mathbf{E}_{P} \left[ \log \frac{p(x)}{q(x)} \right] \]

Khi sử dụng công thức thông tin tương hỗ cho phân phối rời rạc tại từng điểm, chúng ta có thể viết lại công thức trên như sau

\[ D_{KL} (p(X) || q(X)) = \sum_{x \in \mathcal{X}} p(x) \log \frac{p(x)}{q(x)} = \sum_{x \in \mathcal{X}}[-p(x) \log q(x)] - \sum_{x \in \mathcal{X}} [-p(x) \log p(x))] \]

Như vậy, nếu $x$ xuất hiện thường xuyên hơn trong phân phối của $P$ so với mức ta kì vọng ban đầu cho phân phối $Q$, phân kì Kullback - Leibler sẽ lớn hơn và dương; ngược lại, nếu sự xuất hiện đó ít hơn nhiều so với kì vọng ban đầu, phân kì sẽ nhỏ hơn và âm. Như vậy, phân kì Kullback - Leibler là mức độ ngạc nhiên “tương đối” khi quan sát một phân phối mục tiêu, so với phân bố được chọn làm tham chiếu.

Với định nghĩa của phân kì Kullback - Leibler, chúng ta có thể biểu diễn thông tin tương hỗ dưới dạng phân bố hậu nghiệm của $X$ nếu biết giá trị của $Y$ và phân bố tiền nghiệm của $X$, hoặc ngược lại.

\[ I(X;Y) =\mathbf{E}_{Y} [D_{KL} p(X|Y = y) || p(X)] = \mathbf{E}_{X} [D_{KL} p(Y|X = x) || p(Y)] \]

Nói một cách khác, phân kì Kullback - Leibler xác định, về mặt trung bình, sự thay đổi của phân bố $X$ nếu biết giá trị tiền nghiệm của $Y$. Giá trị này là mức độ khác nhau của phân phối kết hợp so với phân phối khi hai biến là độc lập.

\[ I(X;Y) = D_{KL} \left( p(X,Y) || p(X) p(Y) \right) \]

Phân kì Kullback - Leibler còn có thể được diễn giải “đơn giản” như là một sự “bất ngờ không cần thiết” đến từ giá trị thật tiền nghiệm. Giả sử rằng chúng ta có một số $X$ được chọn ngẫu nhiên từ một tập rời rạc với hàm phân bố xác suất $p(x)$. Ví dụ, nếu An biết được phân phối thực sự là $p(x)$, trong khi Bình tin rằng phân phối tiền nghiệm là $q(x)$. Khi đó, nhìn chung, Bình sẽ “bất ngờ” hơn An rất nhiều khi biết được phân phối thật sự của $X$. Phân kì Kullback - Leibler là giá trị kì vọng của sự chênh lệch về độ bất ngờ giữa An và Bình, đo bằng bits nếu logarithm ở cơ số 2. Bằng cách này, phân phối tiền nghiệm của Bình sẽ được định lượng là “lệch” đến mức độ nào bằng độ “bất ngờ không cần thiết” anh ta nhận được.

Mặc dù được thường xuyên sử dụng như một “khoảng cách metric” với giá trị luôn không âm, phân kì Kullback - Leibler không thực sự là một metric do nó không có hai yếu tố cơ bản sau đây: không đối xứng, và không thoả mãn bất đẳng thức tam giác.

Chứng minh tính không âm. Một bài toán thú vị liên quan đến phân kì Kullback - Leibler chính là chứng minh tính không âm của nó cho mọi phân phối $p$, $q$. Để chứng minh điều này, chúng ta áp dụng bất đẳng thức Jensen cho biểu thức của phân kì, dựa trên dữ kiện $f(x) = - \log(x)$ là một hàm lồi. Chứng minh chi tiết được dành lại như một bài tập nhỏ cho bạn đọc.

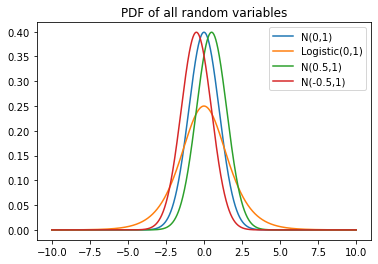
Chúng ta xét ví dụ sau đây để thấy rõ hơn các tính chất của phân kì Kullback - Leibler. Đầu tiên, chúng ta tạo 3 tensor có độ dài 10000

Một tensor thật (mục tiêu) $x$ tuân theo phân phối chuẩn $N(0,1)$;
Ba tensor tiềm năng (dự đoán) $y_1, y_2, y_3$, trong đó
- $y_2$ tuân theo phân phối Logistic $\text{Logistic}(0 ,1)$;
- $y_2$ tuân theo phân phối chuẩn $N(0.5 ,1)$; và
- $y_3$ tuân theo phân phối chuẩn $N(-0.5, 1)$.

import random
import numpy as np
from scipy.stats import norm, logistic
import matplotlib.pyplot as plt

%matplotlib inline

# định nghĩa hàm phân kì Kullback - Leibler
def kl_divergence(p, q):
    return np.sum(np.where(p != 0, x * np.log2(p / q), 0))

# định nghĩa khoảng để viết các hàm mật độ xác suất (PDF)
x_range = np.arange(-10, 10, 0.0001)

# định nghĩa hàm mật độ xác suất (PDF) của các biến tương ứng
x = norm.pdf(x_range, loc=0, scale=1)
y1 = logistic.pdf(x_range, loc=0, scale=1)
y2 = norm.pdf(x_range, loc=0.5, scale=1)
y3 = norm.pdf(x_range, loc=-0.5, scale=1)

# vẽ tất cả các hàm PDF trên cùng một plot
plt.figure()
plt.title('PDF of all random variables')
plt.plot(x_range, x, label = "N(0,1)")
plt.plot(x_range, y1, label = "Logistic(0,1)")
plt.plot(x_range, y2, label = "N(0.5,1)")
plt.plot(x_range, y3, label = "N(-0.5,1)")
plt.legend(loc = "best")
plt.show()

# In các giá trị của phân kì Kullback - Leibler giữa biểu diễn thực và các biểu diễn dự đoán
print("The Kullback - Leibler divergence between N(0,1) and Logistic(0,1) is %.3f"% kl_divergence(x, y1))
print("The Kullback - Leibler divergence between N(0,1) and N(-0.5,1) is %.3f"% kl_divergence(x, y2))
print("The Kullback - Leibler divergence between N(0,1) and N(0.5,1) is %.3f"% kl_divergence(x, y3))

The Kullback - Leibler divergence between N(0,1) and Logistic(0,1) is 2786.996
The Kullback - Leibler divergence between N(0,1) and N(-0.5,1) is 1803.369
The Kullback - Leibler divergence between N(0,1) and N(0.5,1) is 1803.369

assert kl_divergence(x, y1) != kl_divergence(y1, x)
assert kl_divergence(x, y2) != kl_divergence(y2, x)
assert kl_divergence(x, y3) != kl_divergence(y3, x)

Qua ví dụ trên, chúng ta thấy hai tính chất cơ bản như sau:

Giá trị phân kì Kullback - Leibler giữa hai phân phối chuẩn nhỏ hơn khá nhiều so với giữa một phân phối chuẩn và phân phối Logistic; điều này phù hợp với định nghĩa “sự bất ngờ không cần thiết” trong cách diễn giải đơn giản của phân kì.
Giá trị của phân kì Kullback - Leibler là như nhau giữa $N(0,1)$ và $N(0.5, 1)$ hay $N(-0.5, 1)$, bởi vì hai phân phối này đối xứng với nhau qua trục $x = 0$, cũng là giá trị trung bình của phân phối chuẩn thực.
Phân kì Kullback - Leibler không có tính đối xứng, trong bất kì trường hợp nào.

5. Entropy chéo (Cross entropy)¶

5.1. Giới thiệu vấn đề¶

Đầu tiên, chúng ta xét bài toán đơn giản như sau.

Giả sử chúng ta có $n$ điểm dữ liệu cho trước $\{ x_1, x_2, ..., x_n\}$ và một yêu cầu phân loại nhị phân sử dụng mạng neuron với tham số $\theta$. Khi đó, chúng ta tìm $\theta$ tốt nhất để sinh ra các kết quả $\hat{y_i} = p_{\theta} (y_i | x_i)$ tốt nhất.

Với $\pi_i = p_{\theta} (y_i = 1 | x_i)$ và $1 - p_i = p_{\theta} (y_i = 0 | x_i)$, chúng ta viết được hàm log hợp lý như sau

\[\begin{align*} l(\theta) & = \log L(\theta) \\ & = \log \prod_{i=1}^n \pi_i^{y_i} (1 - \pi_i)^{(1 - y_i)} \\ & = \sum_{i=1}^n y_i \log \pi_i + (1 - y_i) \log (1 - \pi_i) \end{align*}\]

Như vậy, cực đại hoá hàm log hợp lý $l(\theta)$ chính là cực tiểu hoá hàm $-l(\theta)$. Để tăng tính khái quát cho tất cả mọi bài toán nhị phân hay đa nhãn, chúng ta gọi $-l(\theta)$ là hàm mất mát entropy chéo (Cross entropy loss), được kí hiệu là $CE(\mathbf{y}, \hat{\mathbf{y}})$, với $\mathbf{y}$ tuân theo phân phối “thật” $P$ và $\hat{\mathbf{y}}$ tuân theo phân phối dự đoán $Q$.

5.2. Định nghĩa Entropy chéo¶

Một lần nữa, chúng ta giả sử rằng tồn tại hai hàm mật độ/khối xác suất cho cùng một biến ngẫu nhiên $X$: $p(x)$ là hàm “thật” ứng với phân phối xác suất $P$ và $q(x)$ là hàm dự đoán với phân phối xác suất $Q$ bất kì.

Hàm entropy chéo của phân phối $Q$ tương ứng với phân phối $P$ được tính như sau

\[ CE(p,q) = - \mathbf{E}_{p} [\log q], \]

với $\mathbf{E}_p$ là hàm kì vọng trên phân phối $p$.

Sử dụng các công thức tính entropy và phân kì Kullback - Leibler $D_{KL} (p||q)$, chúng ta có thể viết lại công thức tính entropy chéo như sau

\[ CE(p,q) = H(p) + D_{KL} (p || q) \]

Với $p, q$ là các hàm phân phối xác suất rời rạc trên cùng một không gian mẫu $X$, công thức này đồng nghĩa với

\[ CE(p,q) = - \sum_{x \in \mathcal{X}} p(x) \log q(x) \]

Trường hợp $p$ và $q$ là các phân phối xác suất liên tục, công thức trên được định nghĩa tương tự. Đầu tiên, chúng ta phải giả sử rằng $p$ và $q$ đều liên tục tuyệt đối với một độ đo tham chiếu $r(x)$ (thông thường, $r(x)$ sẽ là một độ đo Lebesgue hoặc một Borel $\sigma$-algebra). Khi đó, nếu gọi $P(x)$ và $Q(x)$ lần lượt là hàm mật độ xác suất của $p$ với $q$ tương ứng với $r$, chúng ta sẽ có

\[ CE(p,q) = - E_{p} [\log Q] = E_{p} [- \log Q] = - \int_{\mathcal{X}} P(x) \log Q(x) d r(x). \]

Với định nghĩa của entropy chéo, chúng ta có thể nói rằng việc thực hiện những mục tiêu sau là tương đương với nhau:

Cực đại hoá khả năng dự đoán phân phối $P$ từ việc quan sát phân phối $Q$, hay cực đại hoá $E_{p} [\log q(x)]$; tức là, cực tiểu hoá sự “bất ngờ không cần thiết” của việc dự đoán $P$ từ $Q$;
Cực tiểu hoá entropy chéo $CE(p,q)$;
Cực tiểu hoá phân kì Kullback - Leibler $D_{KL} (p(X) || q(X))$.

5.3. Hàm mất mát Entropy chéo (Cross entropy loss) trong bài toán Phân loại Đa lớp¶

Trong phần này, chúng ta sẽ chứng minh được tại sao cực tiểu hoá hàm mất mát entropy chéo lại hương đương với việc cực đại hoá hàm log hợp lý $l$.

Chúng ta xét bài toán như sau. Giả sử chúng ta có tập dữ liệu $\mathbf{x}_i, i = 1, 2, ..., n$ với $n$ mẫu khác nhau được phân vào $k$ tập hợp. Với mỗi phần tử $\mathbf{x}_i$ của dữ liệu, chúng ta lại biểu diễn nhãn của nó dưới dạng $\mathbf{y}_i = (y_{i1}, y_{i2}, ..., y_{in})$ bằng mã hoá one-hot.

Giả sử chúng ta tham số hoá bài toán được giải bằng mạng neuron với tham số $\theta$. Khi đó, dự đoán $\hat{\mathbf{y}_i}$ sẽ bầng

\[ \hat{\mathbf{y}_i} = p_{\theta} (\mathbf{y}_i | \mathbf{x}_i) = \sum_{j=1}^k y_{ij} p_{\theta} (y_{ij} | \mathbf{x}_i) \]

Như vậy, khi đó, hàm entropy chéo giữa giá trị thực và giá trị dự đoán là

\[ CE(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{i=1}^n \mathbf{y}_i \log \hat{\mathbf{y}_i} = - \sum_{i = 1}^n \sum_{j=1}^k y_{ij} \log p_{\theta} (y_{ij} | \mathbf{x}_i) \]

Tương tự với phần giới thiệu vấn đề, giá trị của hàm entropy chéo này chính là nghịch đảo của hàm ước lượng hợp lý cực đại $l(\theta)$ khi giả sử $\mathbf{y}_i$ tuân theo phân phối đa thức $k$ lớp. Như vậy, việc cực đại hoá hàm log hợp lý $l(\theta)$ chính là cực tiểu hoá hàm entropy chéo nêu trên.

Hàm mất mát entropy chéo cho bài toán phân loại đa nhãn có thể được tính trực tiếp, sử dụng hàm log_loss từ thư viện scikit-learn.

from sklearn.metrics import log_loss
true_labels = ["cat", "dog", "dog", "cat"]
pred_proba = [[0.2, 0.8], [0.6, 0.4], [0.75, 0.25], [0.45, 0.55]]
log_loss(true_labels, pred_proba, eps=1e-15)

1.1776326754114792

6. Ứng dụng của lý thuyết thông tin trong các chỉ số đánh giá (metric) cho mô hình phân nhóm (clustering)¶

Như đã nói, lý thuyết thông tin có rất nhiều ứng dụng trong các lĩnh vực khác nhau, một trong số đó là trong việc xây dựng các chỉ số đánh giá cho các mô hình phân nhóm (clustering) hay đa nhãn (classification).

Trong các mô hình học không giám sát (unsupervised learning), có hai loại chỉ số đánh giá được sử dụng, bao gồm

Internal metric: Các chỉ số đánh giá chỉ sử dụng các thông tin sinh ra từ việc chạy thuật toán, bao gồm nhãn dự đoán và tâm (center) của các nhóm được sinh ra. Không có bất kì một thông tin ngoài nào được sử dụng để xây dựng các chỉ số thuộc nhóm này. Nhóm chỉ số này thường được sử dụng trong các bài toán thực tế, khi mà nhãn thực tế của các điểm dữ liệu không có sẵn.
External metric: Các chỉ số đánh giá thuộc nhóm này phải sử dụng một nguồn thông tin ngoài là nhãn dữ liệu “thực” được định sẵn trước đó của tất cả các điểm dữ liệu. Từ nhãn dữ liệu thực, chúng ta có thể biết được rõ ràng rằng kết quả phân nhóm/gán nhãn của chúng ta có hoàn hảo không. Tuy nhiên, việc định lượng xem kết quả chúng ta không chính xác đến đâu là một bài toán phức tạp (Oakes, 1998) và các giải pháp trước đây thường thiếu tính chặt chẽ.

Như vậy, để giải quyết vấn đề của các chỉ số đánh giá thuộc nhóm external, một lớp các chỉ số dựa vào ý tưởng của entropy, hay lý thuyết thông tin nói chung, đã được đề xuất. Những chỉ số thuộc lớp này bao gồm:

Độ hoàn chỉnh (Completeness), Độ đồng nhất (Homogeneity) và VBeta;
Thông tin tương hỗ (Mutual Information - MI) và các biến thể: Thông tin tương hỗ được hiệu chỉnh (Adjusted MI) và Thông tin tương hỗ được chuẩn hoá (Normalized MI);
Q0 và Q0 được chuẩn hoá (Q2).

Trước tiên, trước khi bắt đầu đi vào tính toán các chỉ số đánh giá, chúng ta quy ước như sau:

Tập dữ liệu ban đầu có tổng cộng $N$ điểm dữ liệu;
Có hai cách phân loại tập dữ liệu ban đầu:
- Cách phân loại “thật” $C = \{c_i | i = 1, 2, ..., n \}$;
- Cách phân loại dự đoán $K = \{k_1 | k = 1, 2, ..., m \}$;
- $A$ là bảng liên hợp (contingency table) thể hiện kết qủa của bài toán phân nhóm, trong đó $a_{ij}$ thể hiện số điểm dữ liệu thuộc cả hai nhóm $c_i$ và $k_j$.

Khi đó, entropy và entropy có điều kiện của các phân phối sẽ được tính như sau

Entropy của phân loại “thật”:

\[ H(C) = - \sum_{c = 1}^{|C|} \frac{\sum_{k=1}^{|K|} a_{ck}}{n} \log \frac{\sum_{k=1}^{|K|} a_{ck}}{n} \]

Entropy của phân loại dự đoán:

\[ H(K) = - \sum_{k = 1}^{|K|} \frac{\sum_{c=1}^{|C|} a_{ck}}{n} \log \frac{\sum_{c=1}^{|C|} a_{ck}}{n} \]

Entropy có điều kiện của $C$ với điều kiện $K$ được biết trước:

\[ H(C|K) = - \sum_{k=1}^{|K|} \sum_{c=1}^{|C|} \frac{a_{ck}}{N} \log \frac{a_{ck}}{\sum_{c=1}^{|C|} a_{ck}} \]

Entropy có điều kiện của $K$ với điều kiện $C$ được biết trước:

\[ H(K|C) = - \sum_{c=1}^{|C|} \sum_{k=1}^{|K|} \frac{a_{ck}}{N} \log \frac{a_{ck}}{\sum_{k=1}^{|K|} a_{ck}} \]

6.1. Độ hoàn chỉnh, Độ thống nhất và VBeta¶

Như đã đề cập ở trên, việc định lượng độ không chính xác của kết quả phân nhóm là một bài toán khó. Chính vì vậy, VBeta, được đề xuất bởi Andrew Rosenberg và Julia Hirschberg (2007), là một giải pháp tinh tế cho những vấn đề như sau

Sự phụ thuộc vào thuật toán phân nhóm hoặc dữ liệu ban đầu;
Vấn đề về sự phù hợp, tức là chỉ có một phần nhỏ dữ liệu được phân nhóm được xem xét đến; và
Việc đánh giá chính xác cả hai yếu tố cùng một lúc, sự hoàn chỉnh và sự thống nhất của kết quả.

Hai khái niệm mới, bao gồm độ đồng nhất và độ hoàn chỉnh, đã được đề xuất để đi đến việc tính toán V-Measure.

Độ đồng nhất (Homogeneity)¶

Để thoả mãn tiêu chí về độ đồng nhất, một phân nhóm dự đoán chỉ được nhóm các điểm trong cùng một nhóm ở phân loại “thật”. Tức là, sự phân bố của các nhóm “thật” trong một nhóm được dự đoán phải nghiêng hẳn về một nhóm “thật” nào đó, hay nói cách khác, entropy tiến đến 0.

Chúng ta định nghĩa một phân nhóm dự đoán gần với điều kiện lý tưởng nêu trên như thế nào bằng cách tính entropy có điều kiện của phân nhóm “thật”, giả sử phân nhóm dự đoán được biết trước $H(C|K)$. Tuy nhiên, do giá trị này phụ thuộc vào độ lớn của dữ liệu ban đầu và phân phối của phân loại “thật”, chúng ta sẽ chuẩn hoá giá trị này bằng lượng giảm tối đa thông tin về phân nhóm có thể sản sinh ra, hay $H(C)$.

\[\begin{align*} h = \begin{cases} 1 & \text{ if } H(C,K) = 0 \\ 1 - \frac{H(C|K)}{H(C)} & \text{ else} \end{cases} \end{align*}\]

Độ hoàn chỉnh (Completeness)¶

Độ hoàn chỉnh là một chỉ số đối xứng với độ đồng nhất. Để thoả mãn tiêu chí về độ hoàn chỉnh, một phân nhóm dự đoán phải cố gắng nhóm tất cả các điểm thuộc cùng một nhóm “thật”.

Tương tự như trên, để tính độ hoàn chỉnh, chúng ta xem xét sự phân bố của các phân nhóm dự đoán trong một phân nhóm thật. Tuy nhiên, trong trường hợp xấu nhất, mỗi nhóm thật sẽ được biểu diễn bằng một phân nhóm dự đoán với phân bố giống với phân bố về kích thước của các nhóm, tức là $H(K)$, và chúng ta phải chuẩn hoá độ hoàn chỉnh bằng giá trị này.

\[\begin{align*} c = \begin{cases} 1 & \text{ if } H(K,C) = 0 \\ 1 - \frac{H(K|C)}{H(K)} & \text{ else} \end{cases} \end{align*}\]

VBeta¶

V, viết tắt của “validity” (hợp lệ) trong tiếng Anh, là một thuật ngữ thường được dùng để miêu tả độ chính xác của một kết quả cho bài toán phân nhóm. Như vậy, dựa trên việc tính toán độ đồng nhất và độ hoàn chỉnh ở phía trên, chúng ta tính toán được phép đo độ hợp lý VBeta bằng một hàm trung bình điều hoà (harmonic mean) của hai chỉ số trên như sau

\[ V_{\beta} = \frac{(1 + \beta) \times h \times c}{\beta \times h + c} \]

Như vậy, tương tự như một chỉ số khác là phép đo F (F-Measure), nếu $\beta > 1$, độ hoàn chỉnh sẽ góp phần quan trọng hơn trong phép tính; và ngược lại, nếu $\beta < 1$, độ đồng nhất sẽ đóng vai trò lớn hơn.

Để tính toán độ hoàn chỉnh, độ đồng nhất hay VBeta giữa hai kết quả phân nhóm, chúng ta có thể sử dụng hàm homogeneity_completeness_v_measure trong thư viện scikit-learn để tính cả ba chỉ số cùng một lúc, hoặc từng hàm tương ứng để tính lần lượt từng giá trị.

from sklearn.metrics import homogeneity_completeness_v_measure, \
                            homogeneity_score, \
                            completeness_score, \
                            v_measure_score \

# tạo các nhãn dãn giả thuyết (nhãn dán "thật" và nhãn dán dự đoán)
y_true = [0,0,1,1,2,2]
y_pred = [0,0,0,1,1,2]

# tính toán các chỉ số đánh giá
homogeneity_completeness_v_measure(y_true, y_pred)

# kiểm tra chéo kết quả của các hàm khác nhau
assert homogeneity_completeness_v_measure(y_true, y_pred)[0] == homogeneity_score(y_true, y_pred)
assert homogeneity_completeness_v_measure(y_true, y_pred)[1] == completeness_score(y_true, y_pred)
assert homogeneity_completeness_v_measure(y_true, y_pred)[2] == v_measure_score(y_true, y_pred)

print('Homogeneity score of y_true and y_pred is  %.5f' % homogeneity_score(y_true, y_pred))
print('Completeness score of y_true and y_pred is  %.5f' % completeness_score(y_true, y_pred))
print('The VBeta score of y_true and y_pred with weight 1.0 is %.5f' % v_measure_score(y_true, y_pred))

Homogeneity score of y_true and y_pred is  0.50000
Completeness score of y_true and y_pred is  0.54311
The VBeta score of y_true and y_pred with weight 1.0 is 0.52067

6.2. Thông tin tương hỗ và các biến thể¶

Thông tin tương hỗ được chuẩn hoá (Normalized Mutual Information Score)¶

Thông tin tương hỗ được chuẩn hoá, nói đơn giản, là lượng thông tin tương hỗ được chuẩn hoá để kết quả nhận được nằm trong khoảng 0 (không có thông tin tương hỗ) và 1 (thông tin hoàn toàn trùng khớp).

Trong cách tính của chỉ số này, thông tin tương hỗ sẽ được chuẩn hoá bằng một hàm trung bình tổng quát giữa $H(C)$ và $H(K)$, được định nghĩa bởi tham số average_method. Hàm trung bình tổng quát có 4 dạng khác nhau: giá trị nhỏ nhất (min), giá trị lớn nhất (max), trung bình cộng (arithmetic - được mặc định) và trung bình nhân (geometric).

\[ NMI = \frac{MI}{\text{generalized_average}(H(C), H(K))} \]

Tuy nhiên, một trong những nhược điểm của chỉ số này là không được hiệu chỉnh với các giá trị ngẫu nhiên (adjusted for chance). Khi đó, hàm thông tin tương hỗ được hiệu chỉnh sẽ được sử dụng thường xuyên hơn.

Ngoài ra, chỉ số này còn có tính đối xứng, tức là thay đổi vị trí của y_true và y_pred sẽ không thay đổi giá trị của chỉ số. Điều này hỗ trợ việc so sánh độ tương đồng giữa hai dự đoán khác nhau, khi kết quả phân nhóm “thật” không có sẵn.

Thông tin tương hỗ được hiệu chỉnh (Adjusted Mutual Information Score)¶

Thông tin tương hỗ được hiểu chỉnh là một phiên bản khác của thông tin tương hỗ, nhằm để hiệu chỉnh với những giá trị ngẫu nhiên. Chúng ta dễ dàng nhận thấy rằng giá trị của Thông tin tương hỗ với hai kết quả phân nhóm khác nhau có số lượng các phân nhóm cao hơn, không quan trọng việc chúng có chia sẻ nhiều thông tin với nhau hay không.

Như vậy, chỉ số đánh giá này sẽ được tính như sau

\[ AMI = \frac{MI - \textbf{E}[MI]}{\text{generalized_average}(H(C), H(K)) - \textbf{E}[MI]} \]

Với $\textbf{E}(MI)$, hay giá trị kì vọng của Thông tin tương hỗ, là giá trị cơ sở của lượng thông tin tương hỗ giữa hai kết quả phân nhóm bất kì. Giá trị cơ sở này không nhất thiết phải là một hằng số, và như đã đề cập, sẽ càng cao hơn khi kết quả có càng nhiều phân nhóm. Như vậy, sử dụng một mô hình ngẫu nhiên hyper-geometric, giá trị kì vọng này được tính bằng cách

\[\begin{align*} \mathbf{E}(MI) & = \sum_{i=1}^{|K|} \sum_{i=1}^{|C|} \sum_{n_{ij}=(a_i+b_j-N)^+}^{\min(a_i,b_j)} \frac{n_{ij}}{N} \log \left(\frac{N n_{ij}}{a_i b_j} \right) \\ & \times \frac{a_i! b_j! (N-a_i)! (N-b_j)!}{N! n_{ij}! (a_i - n_{ij})! (b_j - n_{ij})! (N - a_i - b_j + n_{ij})!} \end{align*}\]

với

$(a_i + b_j - N)^+$ biểu diễn $\max(1, a_i + b_j - N)$;
$a_i$ là tổng hàng thứ i của của bảng liên hợp; và
$b_j$ là tổng cột thứ j của bảng liên hợp.

6.3. Q0 và Q0 được chuẩn hoá (Q2)¶

Q0¶

$Q_0$, tương tự như các chỉ số đánh giá khác, cũng sử dụng đại lượng entropy có điều kiện $H(C|K)$ để đo độ tốt của kết quả. Tuy nhiên, như đã được đề cập, đại lượng này chỉ biểu diễn độ đồng nhất của kết quả. Để đánh giá thêm độ hoàn thiện, Dom thêm vào một mô hình hàm giá (model cost term), được tính bằng lập luận của lý thuyết mã hoá. Biểu thức hoàn chỉnh của đại lượng này chính là tổng của hàm entropy có điều kiện và hàm biểu diễn mô hình.

Ý tưởng đằng sau của đánh giá này khá cẩn thận và chi tiết: Với cùng một đại lượng cho enotrpy có điều kiện, kết quả phân nhóm nào sinh ra ít nhóm nhất sẽ được ưu tiên. $$ Q_0(C,K) = H(C|K) + \frac{1}{n} \sum_{k=1}^{|K|} \log \binom{h(K) + |C| - 1}{|C| - 1} $$

Q2¶

$Q_2$ là phiên bản được chuẩn hoá của $Q_0$ nhằm mục đích đưa giá trị của chỉ số đánh giá này về nằm trong khoảng $(0,1]$. Chỉ số đánh giá này càng lớn, kết quả của bài toán phân nhóm càng chính xác và ngược lại.

\[ Q_2(C,K) = \frac{\frac{1}{n} \sum_{c=1}^{|C|} \log \binom{h(C) + |C| - 1}{|C| - 1} }{Q_0(C,K)} \]

7. Bài tập¶

Từ hai kết quả phân nhóm “thật” $C$ và phân nhóm dự đoán $K$ (dưới định dạng numpy arrays), viết hàm tính bảng liên hợp bằng cách sử dụng hàm metrics.contingency_matrix trong thư viện scikit-learn. Từ đó, tính toán các hàm entropy $H(C)$ và $H(K)$, các hàm entropy có điều kiện $H(C|K)$ và $H(K|C)$ theo các công thức đã được cung cấp ở trên.

Ngoài ra, hãy cho biết, trong tất cả các chỉ số đánh giá trong thư viện này, có bao nhiêu thư viện sử dụng/lấy ý tưởng từ lý thuyết thông tin và các phép tính liên quan (entropy/entropy hợp/entropy có điều kiện/thông tin tương hỗ/phân kì KL)?

Để so sánh với kết quả chính xác, với hàm tính entropy, có thử sử dụng chính hàm entropy được lấy từ sklearn.metrics.cluster.
Để tìm số lượng phân nhóm tối ưu cho một bài toán phân nhóm, phương pháp thường dùng nhất chính là phương pháp khuỷu tay (elbow method). Phương pháp này yêu cầu thực hiện thuật toán với số lượng các phân nhóm khác nhau và tính toán kết quả là một chỉ số đánh giá, thường là tổng bình phương giữa các điểm trong cùng phân nhóm (Within-cluster Sum of Squares, WSS). Sau đó, một biểu đồ tương quan giữa số phân nhóm và chỉ số sẽ được thiết lập, và từ biểu đồ này, chúng ta sẽ tìm điểm bẻ cong (điểm khuỷu) để xác định số lượng phân nhóm tối ưu.

Ví dụ, đây là kết quả tính bằng WSS khi thực hiện thuật toán KMeans trên tập dữ liệu USArrests với số phân nhóm từ 1 đến 10. Chúng ta dễ dàng thấy được rằng, điểm bẻ cong sẽ nằm ở $k=2$, do đó, chúng ta quyết định chọn 2 phân nhóm cho bài toán này.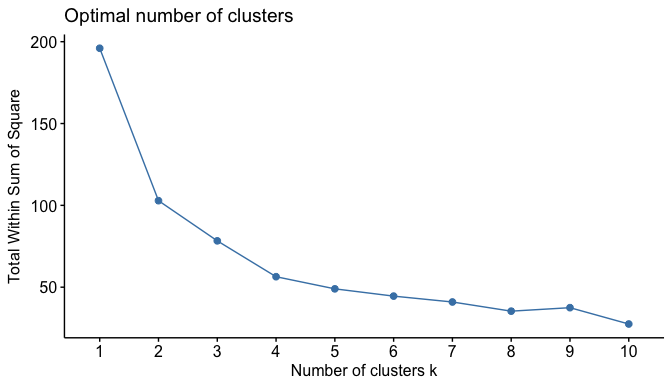

Một cách để cải tiến/thay đổi phương pháp này là thực hiện quy trình tương tự với các chỉ số đánh giá khác nhau. Trong bài tập này, hãy thực hiện quy trình tương tự và thay thế chỉ số WSS bằng các chỉ số đánh giá tiềm năng khác, như Thông tin tương hỗ đã hiệu chỉnh, VBeta hay Q2, giả sử kết quả phân nhóm “thật” đã được cung cấp sẵn. Từ đó, rút ra những ưu và khuyết điểm so với khi thực hiện thuật toán trên chỉ số ban đầu.

Dữ liệu và cách thực hiện thuật toán trong ngôn ngữ thống kê R có thể được tìm thấy tại đây.
Dựa trên hàm metrics.cluster.contingency_matrix được cung cấp sẵn bởi thư viện scikit-learn, hãy viết hàm tính các chỉ số Q0 và Q2.

Để kiểm chứng kết quả của những hàm đã được viết, hiện tại, trong thư viện River, một thư viện được thiết kế cho các mô hình học máy trực tuyến (online ML), đã có các hàm tương tự được viết với mục đích tính toán và cập nhật mô hình với từng cặp kết quả một từ các chuỗi y_true và y_pred. Để kiểm chứng các hàm đã viết, chúng ta thực hiện theo quy trình như sau
- Tạo ra một tập dữ liệu nhỏ (toy dataset) với các điểm dữ liệu và kết quả phân nhóm có sẵn (y_true).
- Chọn một thuật toán phân nhóm, chạy thuật toán đó trên tập dữ liệu được tạo ra và trữ kết quả với biến y_pred.
- Từ thư viện River, cập nhật từng cặp giá trị trong y_true và y_pred vào bảng liên hợp river.metrics.ContingencyMatrix theo hướng dẫn và tính toán các giá trị Q0 và Q2 từ bảng liên hợp đó.
- Tính toán các kết qủa tương ứng bằng các hàm vừa được viết, sau đó so sánh với kết quả tạo ra bởi thư viện River.

8. Tài liệu tham khảo¶

[1] C. E., Shannon. A Mathematical Theory of Communication, Bell System Technical Journal, 27, pp. 379-423 & 623-656, July & October, 1948.

[2] R. V. L., Hartley, Transmission of Information, Bell System Technical Journal, July 1928.

[3] K. P., Burnham, D. R., Anderson. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, Second Edition (Springer Science, New York). ISBN: 978-0-387-95364-9.

[4] H.-A., NGO. Investigation and Implementation of Incremental Clustering Algorithms and Metrics in River, BSc. Thesis at École Polytechnique, IP Paris, France, 2021.

[5] A., Rosenberg, J., Hirschberg. V-Measure: A conditional entropy-based external cluster evaluation measure, Processdings of the 2007 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning, pp. 410-420, Prague, June 2007. URL: https://www.aclweb.org/anthology/D07-1043.pdf

[6] F., Pedregosa et al. Scikit-learn: Machine Learning in Python, JMLR 12, pp. 2825-2830, 2011.

[7] University of Cincinnati Business Analytics. K-Means Cluster Analysis. In: UC Business Analytics R Programming Guide. URL: https://uc-r.github.io/kmeans_clustering

Deep AI KhanhBlog