7.1. Hàm mất mát của SVM¶
7.1.1. Góc nhìn từ hồi qui Logistic¶
Trong hồi qui Logistic chúng ta đã làm quen với hàm mất mát (loss function) dạng:
Bản chất của hàm mất mát trong hồi qui Logistic là một thước đo về sự tương quan giữa phân phối xác suất dự báo với ground truth.
Trong đó phân phối xác suất được ước tính dựa trên hàm Sigmoid theo công thức \(\hat{y} = \sigma(z) = \frac{1}{1+e^{-z}}\).
Ta cũng biết rằng đường biên phân loại của hồi qui Logistic là một siêu phẳng có phương trình \(\mathbf{w}^{\intercal}\mathbf{x}\).
Tiếp theo chúng ta sẽ cùng phân tích hàm mất mát của mô hình trong hai trường hợp \(y=0\) và \(y=1\):
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 2, figsize = (18, 6))
z = np.linspace(-3, 3, 100)
def sigmoid(z):
return 1/(1+np.exp(-z))
y0 = -np.log(1-sigmoid(z)) # Trường hợp ground truth = 0
y1 = -np.log(sigmoid(z)) # Trường hợp ground truth = 1
# Hàm mất mát nếu ground truth = 1
ax[0].plot(z, y1)
ax[0].set_xlabel('z')
ax[0].set_ylabel('L(y, yhat)')
ax[0].set_title('y=1')
# Hàm mất mát nếu ground truth = 0
ax[1].plot(z, y0)
ax[1].set_xlabel('z')
ax[1].set_ylabel('L(y, yhat)')
ax[1].set_title('y=0')
plt.show()
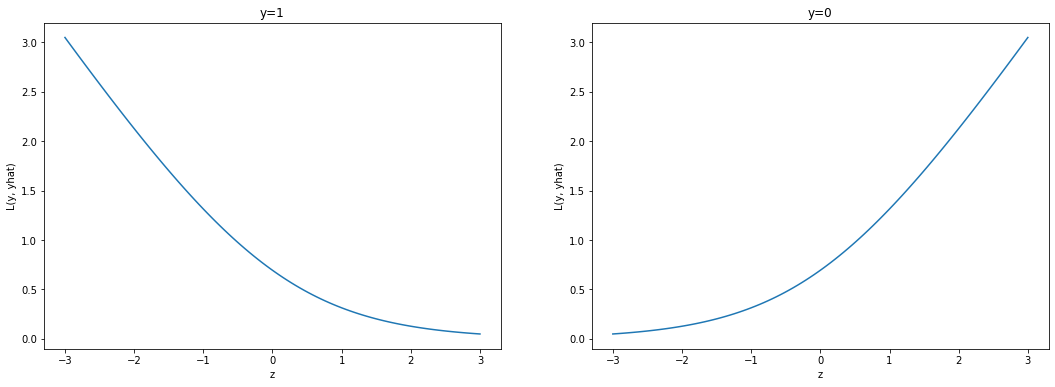
Ta nhận thấy hình dạng của hàm mất mát trong hai trường hợp tương ứng với \(y=1\) và \(y=0\) là trái ngược nhau:
Đối với trường hợp nhãn \(y = 1\): Khi giá trị của \(z\) càng lớn thì hàm mất mát sẽ tiệm cận 0. Điều đó đồng nghĩa với mô hình sẽ phạt ít những trường hợp \(z\) lớn và có nhãn 0. Những trường hợp này tương ứng với những điểm nằm cách xa đường biên phân chia.
Đối với nhãn \(y=0\) thì trái lại, mô hình có xu hướng phạt ít với những giá trị \(z\) nhỏ. Khi đó những điểm này sẽ nằm cách xa đường biên về phía nửa mặt phẳng \(y=1\).
Những phân tích ở trên là hợp lý vì ở các mức giá trị \(z\) đủ lớn hoặc đủ nhỏ thì đều là các điểm nằm cách xa đường biên phân chia nên chúng ta có thể dễ dàng dự báo đúng nhãn cho chúng. Việc phạt những điểm này nếu phân loại sai không mang nhiều ý nghĩa bằng phạt những điểm nằm gần đường biên và được xem như là case khó (hard case). Thậm chí nếu phạt những điểm nằm xa đường biên một giá trị lớn dễ khiến xảy ra nguy cơ quá khớp vì hầu hết những điểm đó đều là ngoại lai.
7.1.2. Từ Logistic tới SVM¶
Trong SVM chúng ta có một thay đổi đột phá đó là tìm cách xấp xỉ hàm mất mát dạng cross-entropy của Logistic bằng một hàm mà chỉ phạt những điểm ở gần đường biên thay vì phạt những điểm ở xa đường biên bằng cách đưa mức phạt về 0.
Cụ thể đó là hai hàm phạt \(\text{cost}_1()\) và \(\text{cost}_2()\) tương ứng với \(y=0\) và \(y=1\) như bên dưới:
Hai hàm này thể hiện chi phí phải bỏ ra nếu phân loại sai các nhãn lần lượt thuộc \(0\) hoặc \(1\). Dạng tổng quát của chúng là \(\max(0, t)\) còn được gọi là hàm hingloss. Đây là một trong những hàm mất mát mà bạn sẽ gặp khá nhiều trong machine learning.
Bên dưới là hình dạng của hai hàm \(\text{cost}_1()\) và \(\text{cost}_2()\).
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 2, figsize = (18, 6))
z = np.linspace(-3, 3, 100)
def sigmoid(z):
return 1/(1+np.exp(-z))
y0 = -np.log(1-sigmoid(z)) # Trường hợp ground truth = 0
y1 = -np.log(sigmoid(z)) # Trường hợp ground truth = 1
cost1 = np.maximum(1+z, 0) # Trường hợp ground truth = 0
cost2 = np.maximum(0, 1-z) # Trường hợp ground truth = 1
# Hàm mất mát nếu ground truth = 1
ax[0].plot(z, y1)
ax[0].plot(z, cost2)
ax[0].set_xlabel('z')
ax[0].set_ylabel('L(y, yhat)')
ax[0].legend(labels = ['cross-entropy', 'cost2'])
ax[0].set_title('y=1')
# Hàm mất mát nếu ground truth = 0
ax[1].plot(z, y0)
ax[1].plot(z, cost1)
ax[1].set_xlabel('z')
ax[1].set_ylabel('L(y, yhat)')
ax[1].legend(labels = ['cross-entropy', 'cost1'])
ax[1].set_title('y=0')
plt.show()
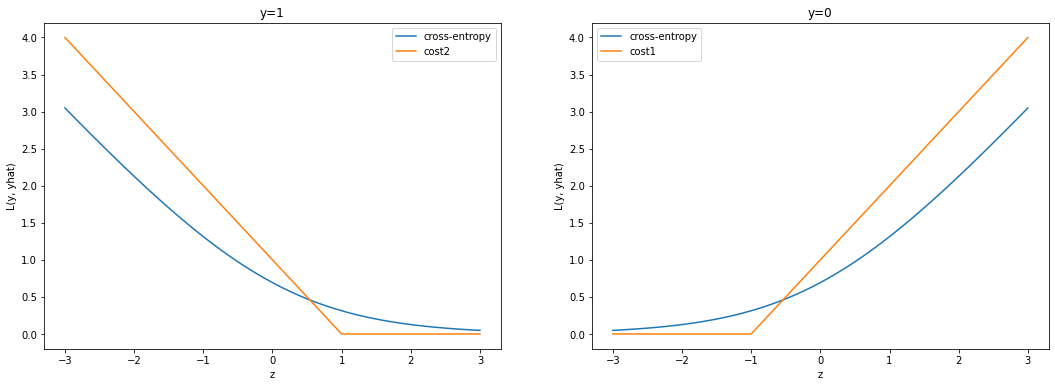
Ta nhận thấy hình dạng của các hàm mất mát \(\text{cost}_1\) và \(\text{cost}_2\) cũng gần tương tự như cross-entropy. Điểm khác biệt chính đó là giá trị của mất mát bằng 0 nếu \(z \geq 1\) (đối với nhãn \(y=1\)) hoặc \(z \leq -1\) (đối với nhãn \(y=0\)). Theo các hàm mất mát mới này, chúng ta bỏ qua việc phạt phân loại sai những điểm nằm xa đường biên. Đối với những điểm nằm gần đường biên nhất thì mới ảnh hưởng tới hàm mất mát. Tập hợp những điểm nằm gần đường biên sẽ giúp xác định đường biên và được gọi là tập tập hỗ trợ (support vector).
Như vậy sau khi thay đổi hàm phạt ta thu được hàm mất mát mới dạng:
SVM cho phép ta giảm thiểu quá khớp thông qua một thành phần điều chuẩn cũng tương tự như hồi qui Logistic.
Trong công thức trên thì hằng số \(C > 0\) thể hiện ảnh hưởng của sai số phân loại lên hàm mất mát. Trong khi \(\lambda > 0\) là hằng số của thành phần điều chuẩn (regularization term) thể hiện tác động của độ lớn trọng số hồi qui \(\mathbf{w}\) lên hàm mất mát.
Khi tăng tỷ lệ \(\frac{\lambda}{C}\) có thể giúp các trọng số của mô hình được kiểm soát về độ lớn, thông qua đó làm cho độ phức tạp của đường biên phân chia giảm và kiểm soát hiện tượng quá khớp.
Đối với phương trình hồi qui Logistic thì chúng ta sẽ xác định nhãn dựa trên dấu của \(\mathbf{w}^{\intercal}\mathbf{x}\). Còn trong thuật toán SVM, đối với một tập dữ liệu mà các nhãn là phân tuyến (linear seperable) (tức là tồn tại ít nhất 1 đường biên phân loại đúng toàn bộ các điểm) thì chúng ta sẽ mở rộng đường biên phân chia về hai phía là 1 đơn vị. Khi đó một điểm được dự báo là:
Ý nghĩa của việc mở rộng đường biên đó là khiến cho các điểm nằm gần với đường biên sẽ trở nên tách biệt hơn. Tiếp theo chúng ta sẽ tìm hiểu cơ chế nào hoạt động và cách xác định đường biên đối với thuật toán SVM.
7.2. Đường biên và lề trong SVM¶
Tập dữ liệu của bài toán SVM
Giả sử tập dữ liệu huấn luyện \(\mathcal{Z}\) bao gồm \(N\) điểm dữ liệu. Trong đó điểm dữ liệu thứ \(i\) là \(Z_i = (\mathbf{x}_i, y_i)\) với \(\mathbf{x}_i \in \mathbb{R}^{d}\) là véc tơ đầu vào và \(y_i\) là biến mục tiêu là một trong hai giá trị \(\{-1, 1\}\). Tập dữ liệu này được giả định là phân tuyến (linear seperable).
Bên dưới là hình ảnh tập dữ liệu phân tuyến, đường biên và lề trong thuật toán SVM.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs
# we create 40 separable points
X, y = make_blobs(n_samples=40, centers=[(0, 3), (3, 0)], cluster_std=[0.5, 0.5], random_state=6)
idx_cls_0 = np.where(y == 0)
idx_cls_1 = np.where(y == 1)
# fit the model, don't regularize for illustration purposes
clf = svm.SVC(kernel='linear', C=1000)
clf.fit(X, y)
plt.figure(figsize = (12, 8))
plt.scatter(X[idx_cls_0, 0], X[idx_cls_0, 1], c='red', marker='o', s=50)
plt.scatter(X[idx_cls_1, 0], X[idx_cls_1, 1], c='blue', marker='*', s=100)
# plot the decision function
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
B = clf.decision_function(xy).reshape(XX.shape)
A = B-0.9
C = B+0.8
# plot decision boundary and margins
ax.contour(XX, YY, B, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
ax.contour(XX, YY, A, colors='k', levels=[0], alpha=0.5,
linestyles=['-'])
ax.contour(XX, YY, C, colors='k', levels=[0], alpha=0.5,
linestyles=['-'])
# plot support vectors
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,
marker='o',linewidth=1, facecolors='none', edgecolors='k')
ax.text(0, -0.5, 'B', fontsize=18)
ax.text(-1, -0.5, 'A', fontsize=18)
ax.text(1, -0.5, 'C', fontsize=18)
plt.show()
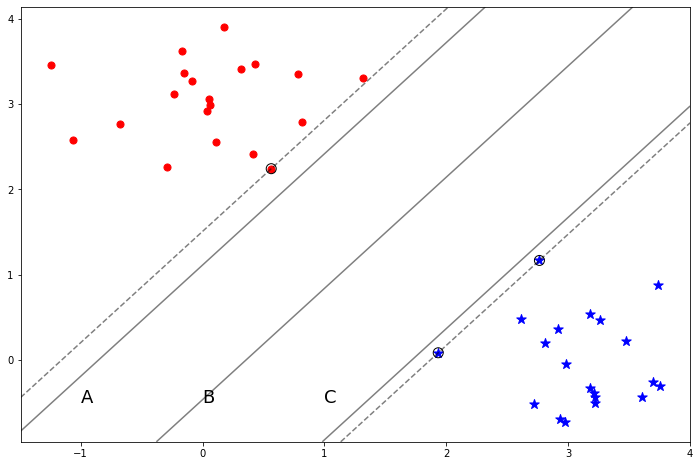
Hình 1: Hình ảnh về tập dữ liệu trong bài toán phân loại nhị phân mà các lớp là phân tuyến. Ba đường thẳng A, B, C đại diện cho ba đường biên phân chia đúng mọi điểm dữ liệu. Những điểm hình tròn nằm bên trái thuộc mặt dương có nhãn \(y=1\), những điểm hình sao nhằm bên phải thuộc mặt âm nhãn \(y=-1\). Sở dĩ chúng ta gán nhãn như vậy là vì tại cùng một dữ liệu đầu vào \(\mathbf{x}\) thì mặt dương bên trái sẽ có giá trị lớn hơn mặt âm bên phải.
Lựa chọn đường biên phân chia tương ứng với một phương
Ba đường thẳng A, B, C ở ví dụ trên là ba đường biên phân chia song song và có cùng phương. Trong ba đường biên phân chia thì đường biên B là công bằng nhất vì chúng cách đều các điểm gần nhất thuộc hai lớp. Còn lựa chọn A và C sẽ không công bằng vì chúng ta sẽ dễ thiên vị một lớp hơn lớp còn lại.
Như vậy để cho công bằng thì đường biên phải luôn nằm chính giữa và cách đều các điểm gần nhất với nó. Đồng thời đối với bài toán Hard-Margin SVM thì tập dữ liệu là phân tuyến nên đường biên cần phải phân loại đúng mọi điểm dữ liệu. Chúng ta coi độ rộng của đường biên là lề (margin). Ngoài ra tập hợp những điểm nằm sát đường biên nhất thì được gọi là tập hỗ trợ. Những điểm này sẽ hỗ trợ tìm ra đường biên vì những đường thẳng nét đứt đi qua chúng song song với đường biên.
Trong không gian hai chiều thì đường biên là một đường thẳng. Trong không gian 3 chiều chúng sẽ là một mặt phẳng (plane). Trong không gian nhiều hơn 3 chiều chúng ta gọi đường biên phân chia là siêu phẳng (hyperplane).
Một câu hỏi đặt ra đó là có vô số những đường biên phân loại, vậy thì đường biên nào là phù hợp nhất?
Mục tiêu của SVM đó là tìm ra một siêu phẳng (hyperplane) trong không gian \(d\) chiều làm đường biên phân chia sao cho độ rộng lề của chúng là lớn nhất vì khi phân chia theo đường biên này thì các nhóm là tách biệt nhất.

Hình 2: Hình ảnh các trường hợp của đường biên phân chia với các phương khác nhau đối với một tập dữ liệu phân tuyến. Các đường nét đậm (\(B\) và \(D\)) được gọi là đường biên dùng để xác định nhãn dự báo. Các đường nét nhạt đối xứng về hai phía qua đường biên được gọi là mép của lề và khoảng cách độ rộng từ mép của lề tới đường biên được gọi là lề (margin). Những điểm được khoanh tròn gần với vị trí của đường biên nhất sẽ được sử dụng để xác định mép của lề (ta sẽ chứng minh đều này ở bài toán đối ngẫu SVM) và thông qua đó xác định đường biên, tập hợp những điểm này được gọi là tập hỗ trợ \(S\) (support vector). Một đường biên phân chia càng tốt hai tập dữ liệu nếu như độ rộng lề càng lớn.
Khoảng cách từ một điểm tới một siêu phẳng
Giả sử phương trình của đường biên phân chia hai điểm dữ liệu là:
\(b\) là hệ số tự do, \(\mathbf{w}\) là các véc tơ hệ số. \(\mathbf{x}\) là véc tơ quan sát đầu vào.
Trong chương trình THPT chúng ta đã được học về công thức khoảng cách từ một điểm \(A = (x_1, x_2)\) tới một đường thẳng \(l\) có phương trình \(b + w_1 x_1 + w_2 x_2 = 0\) là:
Trong trường hợp tổng quát, khoảng cách từ một điểm bất kỳ \(Z_i = (\mathbf{x}_i, y_i)\) tới đường biên là siêu phẳng \(H\) có phương trình \(b+\mathbf{w}^{\intercal}\mathbf{x} = 0\) sẽ là:
Trong công thức trên thì \(|b+\mathbf{w}^{\intercal}\mathbf{x}| = y_i(b+\mathbf{w}^{\intercal}\mathbf{x}_i)\) là vì:
Xét trường hợp nhãn \(y_i=-1\) thì điểm \(Z_i\) nằm ở mặt âm và có \(b+\mathbf{w}^{\intercal}\mathbf{x}_i \leq 0\). Do đó \(y_i(b+\mathbf{w}^{\intercal}\mathbf{x}_i) \geq 0\).
Xét trường hợp nhãn \(y_i = 1\) thì \(Z_i\) nằm ở mặt dương và có \(b+\mathbf{w}^{\intercal}\mathbf{x}_i \geq 0\). Từ đó suy ra \(y_i(b+\mathbf{w}^{\intercal}\mathbf{x}_i) \geq 0\).
Trong cả hai trường hợp thì đẳng thức \(|b+\mathbf{w}^{\intercal}\mathbf{x}| = y_i(b+\mathbf{w}^{\intercal}\mathbf{x}_i)\) luôn xảy ra.
Tìm đường biên có lề lớn nhất
Tập hợp các điểm nằm gần nhất với một đường biên sẽ giúp xác định phương trình đường biên nên chúng còn được gọi là tập hợp các điểm hỗ trợ (support points), ký hiệu là \(\mathcal{S}\). Trong hình 2 thì các điểm được khoanh tròn chính là các điểm thuộc tập hỗ trợ. Để tìm ra đường biên có độ rộng lề là lớn nhất thì chúng ta cần tối đa hoá khoảng cách từ các điểm thuộc tập hỗ trợ tới đường biên. Điều này tương đương với giải bài toán tối ưu:
Khi nhân vào phương trình đường biên với một hệ số \(k\) thì đường biên không thay đổi. Do đó khoảng cách từ mọi điểm tới đường biên không thay đổi. Tức là khoảng cách từ các điểm thuộc tập hỗ trợ tới đường biên không thay đổi và dẫn tới độ rộng của lề là không thay đổi. Nhờ tính chất này chúng ta có thể nhân thêm vào các trọng số \(w_i\) của phương trình đường biên một hệ số \(k\) sao cho với các điểm dữ liệu thuộc tập hỗ trợ \(\mathcal{S}\) thì \(b+y_i(\mathbf{w}^{\intercal}\mathbf{x}_i) = 1\). Điều đó cũng đồng nghĩa với luôn tìm được một cách nhân với \(k\) sao cho đường biên:
Thay vào \((1)\) thì bài toán tìm nghiệm \(\hat{\mathbf{w}}, \hat{b}\) tương ứng với bài toán tối ưu với ràng buộc tuyến tính:
Điều kiện ràng buộc \(y_i(b+\mathbf{w}^{\intercal}\mathbf{x}_i) \geq 1, \forall i=\overline{1, N}\) là vì khoảng cách từ mọi điểm luôn lớn hơn khoảng cách từ các điểm hỗ trợ tới đường biên phân chia và khoảng cách này bằng 1 vì theo giả định ta đã nhân với hệ số \(k\) vào phương trình đường biên.
Để đơn giản hoá thì bài toán tối ưu \((2)\) có thể nghịch đảo hàm mục tiêu để chuyển sang dạng tương đương:
Hàm mục tiêu chúng ta lấy bình phương là để dễ dàng tính đạo hàm. Bài toán tối ưu \((3)\) là một bài toán tối ưu lồi QP khá quen thuộc. Bài toán này có hệ điều kiện ràng buộc tuyến tính và chúng ta có thể giải thông qua hệ điều kiện KKT.
7.3. Bài toán tối ưu SVM¶
7.3.1. Hệ điều kiện KKT¶
Giả sử chúng ta đang cần giải quyết bài toán tối ưu:
Thoả mãn hệ ĐK ràng buộc:
Bài toán tối ưu có hàm mục tiêu và hệ điều kiện ràng buộc còn được gọi là bài toán gốc (primal problem). Để giải trực tiếp bài toán gốc là tương đối khó nên chúng ta sẽ chuyển sang giải bài toán tối ưu trên hàm đối ngẫu Lagrange (Lagrange Dual Function).
Trong đó \(\lambda_i > 0 ~ \forall i\) và \(\nu_j > 0 ~ \forall j\), những hệ số này còn được gọi là những nhân tử Lagrange (Lagrange Multipliers).
Bằng cách thiết lập phương trình đạo hàm bậc nhất của hàm Lagrange kết hợp với hệ điều kiện ràng buộc tuyến tính và một số điều kiện khác ta có thể thu được nghiệm của bài toán tối ưu. Hệ điều kiện này được gọi là Karush-Kuhn-Tucker conditions (viết tắt là KKT conditions). Trong tối ưu có rất nhiều các bài toán được giải quyết thông qua hệ điều kiện KKT. Đây là một trong những tiêu chuẩn tìm nghiệm khá hiệu quả và thường được sử dụng trong những bài toán tối ưu có điều kiện ràng buộc. Hệ điều kiện KKT bao gồm các nhóm điều kiện:
Stationary: \(\nabla_{\mathbf{x}} f(\mathbf{x}) + \sum_{i=1}^{m}\lambda_i \nabla_{\mathbf{x}} h_i(\mathbf{x}) + \sum_{i=1}^{n} \nu_j \nabla_{\mathbf{x}} g_j(\mathbf{x}) = 0\)
Complenatery slackness: \(\nu_j g_j(\mathbf{x}) = 0, ~~ \forall j\)
Primal Feasibility: \(h_i(\mathbf{x}) = 0, g_j(\mathbf{x}) \leq 0, ~~\forall i, j\).
Dual Feasibility: \(\nu_i \geq 0, ~~ \forall i\).
Giả sử bài toán là strong duality. Khi đó nghiệm \(\mathbf{x}^*\) của hàm đối ngẫu Lagrange cũng là nghiệm của bài toán gốc. Điều kiện cần để hàm mục tiêu đạt được cực trị tại \(\mathbf{x}^*\) là đạo hàm bậc nhất bằng 0. Đây chính là điều kiện stationary ở trên.
Không phải khi nào thì ràng buộc dạng bất phương trình đều được thoả mãn. Đối với những bất phương trình không được thoả mãn thì để cực tiểu của hàm Lagrange bằng cực tiểu của bài toán gốc thì \(\nu_j g_j(\mathbf{x}) = 0, ~ \forall j\). Đây chính là điều kiện complenatery slackness.
Để hàm Lagrange là cận dưới của hàm mục tiêu trong bài toán gốc thì hệ số của những ràng buộc bất phương trình phải thoả mãn \(\nu_i \geq 0\) tương đương với điều kiện dual feasibility.
Ngoài ra, hệ điều kiện ràng buộc phương trình và bất phương trình của bài toán gốc chính cũng cần được thoả mãn. Tức là điều kiện primal feasibility được thoả mãn.
7.3.2. Bài toán tối ưu bậc hai (Quadratic Optimization)¶
Ví dụ về bài toán tối ưu Quadratic Program
Quadratic Program (viết tắt là QP) là một bài toán khá điển hiển hình trong tối ưu hoá và được sử dụng nhiều trong Machine Learning. Đây là dạng bài toán tối ưu xuất hiện trong mô hình SVM. Để hiểu về bài toán tối ưu QP là gì, chúng ta làm quen với một ví dụ đơn giản về tìm cực tiểu như bên dưới:
Thoả mãn:
Lời giải cho bài toán khá dễ dàng nhờ khai triển đẳng thức:
Tuy nhiên cách giải trên là không tổng quát bởi không phải khi nào chúng ta cũng may mắn tìm được lời giải như trên.
Dạng tổng quát cho tối ưu Quadratic Program
Trong tối ưu thì dạng khái quát cho bài toán trên chính là bài toán tối ưu QP có hàm mục tiêu bậc hai:
Thoả mãn hệ điều kiện ràng buộc tuyến tính:
Trong đó ma trận \(\mathbf{A} \in \mathbb{S}^{d}_{+}\) là một ma trận đối xứng bán xác định dương. \(\mathbf{H} \in \mathbb{R}^{M\times d}, \mathbf{G} \in \mathbb{R}^{N\times d}\) lần lượt là những ma trận hệ số của hệ phương trình và bất phương trình ràng buộc tuyến tính. \(\mathbf{x}\) là véc tơ đầu vào kích thước là \(d\). Nếu bạn chưa biết về ma trận bán xác định dương thì đây chính là ma trận mà với mọi véc tơ \(\mathbf{x}\) thì \(\mathbf{x}^{\intercal}\mathbf{A}\mathbf{x} \geq 0, \forall \mathbf{x}\in \mathbb{R}^{d}\), chúng ta kí hiệu là \(\mathbf{A} \succeq 0\).
Giả sử \(a_{ij}\) chính là phần tử thuộc dòng thứ \(i\) và cột thứ \(j\) của ma trận \(\mathbf{A}\). Nếu tinh ý bạn sẽ thấy \(\mathbf{x}^{\intercal}\mathbf{A}\mathbf{x} = \sum_{i=1}^{d}\sum_{j=1}^{d} a_{ij} x_i x_j = a_{ii}x_i^2 + (a_{ij}+a_{ji})x_{ij}\) chính là một đa thức bậc hai giữa tổng các bình phương và tích chéo của biến đầu vào. Thành phần này sẽ khái quát cho \(5x^2+6xy+2y^2\) trong bài toán \((4)\). Trong khi đó \(\mathbf{b}^{\intercal}\mathbf{x}\) tương ứng với \(4x+2y\) và hằng số \(c\) tương ứng với 1.
Lý do trong bài toán QP chúng ta lại cần \(\mathbf{A}\) là ma trận bán xác định dương là vì khi đó đạo hàm bậc 2 của hàm mục tiêu \(\nabla_{\mathbf{x}}^2 ~~ [\frac{1}{2}\mathbf{x}^{\intercal}\mathbf{A}\mathbf{x} + \mathbf{b}^{\intercal}\mathbf{x} + c] = (\mathbf{A} + \mathbf{A}^{\intercal}) \succeq 0\) . Do đó hàm mục tiêu là một hàm lồi.
Nếu hàm mục tiêu là lồi và tồn tại một véc tơ \(\mathbf{x}^*\) sao cho \(\mathbf{H}\mathbf{x}^*=\mathbf{d}\) và \(\mathbf{G}\mathbf{x}^* \prec \mathbf{e}\) thì ta nói bài toán gốc thoả mãn tiêu chuẩn Slater (Slater’s condition). Khi đó bài toán đối ngẫu là một bài toán strong duality và giá trị cực tiểu của bài toán gốc (primal problem) và bài toán đối ngẫu (dual problem) là bằng nhau. Thông thường thì trong các bài toán tối ưu QP với hệ điều kiện ràng buộc tuyến tính và hàm mục tiêu là một hàm lồi thì tiêu chuẩn Slater thường xuyên xảy ra. Điều đó giúp ta có thể tìm được nghiệm cho bài toán tối ưu thông qua bài toán đối ngẫu.
7.3.3. Hệ điều kiện KKT đối với bài toán Quadratic¶
Bài toán tối ưu có hàm mục tiêu và hệ điều kiện ràng buộc còn được gọi là bài toán gốc (primal problem). Để giải trực tiếp bài toán gốc là tương đối khó nên chúng ta sẽ chuyển sang giải bài toán tối ưu trên hàm đối ngẫu Lagrange (Lagrange Dual Function).
Trong đó \(\lambda, \nu\) là những véc tơ hệ số có kích thước lần lượt bằng với số lượng các điều kiện ràng buộc phương trình và bất phương trình và có gía trị lớn hơn hoặc bằng 0. Trong trường hợp bài toán gốc không tồn tại hệ điều kiện bất phương trình thì hàm đối ngẫu Lagrange có dạng:
Ta dễ dàng nhận thấy ưu điểm của hàm đối ngẫu \(g(\lambda, \nu)\) so với hàm mục tiêu gốc đó là:
Là một hàm lồi bất kể hàm mục tiêu gốc có là hàm lồi hay không. Nếu tinh tế ta có thể nhận ra hàm đối ngẫu chính là cận dưới infimum của hàm mục tiêu gốc.
Trong điều kiện tồn tại \(\mathbf{x}^*\) sao cho \(\mathbf{H}\mathbf{x}^{*} = \mathbf{d}\) và \(\mathbf{G}\mathbf{x}^* \prec \mathbf{e}\) thì chúng ta nói tiêu chuẩn Slatter được thoả mãn. Bài toán đối ngẫu khi thoả mãn tiêu chuẩn Slatter sẽ là một bài toán đối ngẫu mạnh (strong duality). Khi đó hệ điều kiện KKT là điều kiện cần và cũng là điều kiện đủ và giá trị cực tiểu \(f^* = g^*\).
Bài toán đối ngẫu có thể được giải thông qua hệ điều kiện KKT. Đối với bài toán tối ưu QP không tồn tại hệ điều kiện ràng buộc bất phương trình thì có hệ điều kiện KKT như bên dưới:
Dòng thứ nhất của phương trình ma trận trên sẽ tương ứng với đạo hàm bậc nhất Lagrange bằng 0:
Dòng thứ 2 chính là phương trình ràng buộc.
Để giải bài toán tối ưu QP có thể sử dụng package cvxopt trong python. Đây là một package chuyên biệt giúp giải quyết các bài toán tối ưu lồi.
7.3.4. Bài toán đối ngẫu SVM¶
Bài toán tối ưu \((3)\) chính là một bài toán QP tương ứng với:
\(\mathbf{A}\) là ma trận đơn vị.
\(\mathbf{b}\) là véc tơ 0.
Ma trận ràng buộc \(\mathbf{G} \in \mathbb{R}^{N \times d}\) có các dòng chính là các điều kiện ràng buộc \(y_i(b+\mathbf{w}^{\intercal}\mathbf{x})\geq 1\).
Hàm đối ngẫu trong bài toán tối ưu ở \((3)\):
Nghiệm tối ưu của hàm Lagrange \((5)\) có thể được tìm thông qua đạo hàm bậc nhất:
Bằng một số phép biến đổi đơn giản trên hàm đối ngẫu ta thu được một biểu thức ngắn gọn.
Theo hệ điều kiện KKT thì giá trị cực tiểu của hàm \(g(\lambda)\) đạt được khi \(\sum_{i=1}^N \lambda_i(1 - y_i(\mathbf{w}^{\intercal}\mathbf{x}_i + b) ) = 0\). Đẳng thức trên đạt được khi \(\lambda_i = 0\) hoặc \(1-y_i(\mathbf{w}^{\intercal}\mathbf{x}_i + b) = 0, ~ \forall i=\overline{1,N}\). Trên thực tế thì véc tơ \(\lambda\) là một véc tơ thưa có hầu hết các chiều đều bằng 0. Đối với những điểm dữ liệu tương ứng với \(\lambda_i > 0\) thì phương trình \(1 - y_i(\mathbf{w}^{\intercal}\mathbf{x}_i + b) = 0\) sẽ được thoả mãn và tập hợp những điểm này khi đó sẽ nằm trên mép của lề. Tập hợp những điểm này còn gọi là tập hỗ trợ (support vector) và được kí hiệu là \(\mathcal{S}\).
Phương trình \((6)\) cho chúng ta biết rằng tập hợp các điểm thuộc tập hỗ trợ có thể giúp ta tính ra \(\mathbf{w}\). Thật vậy:
Ngoài ra đối với toàn bộ các điểm thuộc tập hỗ trợ thì:
Như vậy sau khi tính được \(\mathbf{w}\) thì ta suy ra giá trị của \(b\):
7.3.5. Dự báo nhãn¶
Nhãn của một quan sát trong mô hình SVM sẽ phụ thuộc vào dấu của đường biên:
Trong trường hợp \(h_{\mathbf{w}, b}(\mathbf{x}_i) > 0\) thì điểm được dự báo nhãn \(1\) và trái lại là nhãn \(-1\).
Từ dòng thứ \(1\) sang dòng thứ \(2\) là vì giá trị \(\mathbf{w}\) được tính trực tiếp từ tập hỗ trợ. Công thức trên cho thấy thay vì phải xác định nhãn dựa trên các hệ số của phương trình đường biên \(\mathbf{w}\) thì chúng ta có thể thông qua các điểm thuộc tập hỗ trợ.
7.4. Sorf Margin Classification¶
7.4.1. So sánh giữa lề cứng (hard margin) và lề mềm (soft margin)¶
Đường biên phân chia của thuật toán SVM sẽ chịu ảnh hưởng bởi những điểm thuộc tập hỗ trợ \(\mathcal{S}\). Trong trường hợp đường biên phân chia đúng mọi điểm điểm dữ liệu thì được gọi là bài toán phân loại theo đường biên cứng (hard margin classification). Tuy nhiên đường biên cứng tỏ ra hạn chế nếu tồn tại dữ liệu ngoại lai (outlier). Chúng ta cùng phân tích hạn chế này ở hình minh hoạ bên dưới.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from sklearn import svm
# we create 40 separable points
X, y = make_blobs(n_samples=40, centers=[(0, 3), (3, 0)], cluster_std=[0.5, 0.5], random_state=6)
idx_cls_0 = np.where(y == 0)
idx_cls_1 = np.where(y == 1)
id_max = np.argmax(X, axis=0)
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
# fit the model
for i in range(2):
# Adjust outlier
if i == 1:
X[id_max[0]] = [1, 2]
clf = svm.SVC(kernel='linear', C=100)
clf.fit(X, y)
# get the separating hyperplane
w = clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-5, 5)
yy = a * xx - (clf.intercept_[0]) / w[1]
# plot the parallels to the separating hyperplane that pass through the
# support vectors (margin away from hyperplane in direction
# perpendicular to hyperplane). This is sqrt(1+a^2) away vertically in
# 2-d.
margin = 1 / np.sqrt(np.sum(clf.coef_ ** 2))
yy_down = yy - np.sqrt(1 + a ** 2) * margin
yy_up = yy + np.sqrt(1 + a ** 2) * margin
# plot the line, the points, and the nearest vectors to the plane
ax[i].plot(xx, yy, 'k-')
ax[i].plot(xx, yy_down, 'k--')
ax[i].plot(xx, yy_up, 'k--')
ax[i].scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80,
facecolors='none', zorder=10, edgecolors='k',
cmap=cm.get_cmap('RdBu'))
ax[i].scatter(X[idx_cls_0, 0], X[idx_cls_0, 1], c='red', marker='o', s=50)
ax[i].scatter(X[idx_cls_1, 0], X[idx_cls_1, 1], c='blue', marker='*', s=100)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
x_min = -1.5
x_max = 4
y_min = -1
y_max = 4
# Put the result into a contour plot
ax[i].contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
ax[i].set_xlim(x_min, x_max)
ax[i].set_ylim(y_min, y_max)
if i == 0:
ax[i].set_title('Hard Margin SVM')
else:
ax[i].set_title('Hard Margin SVM with Outlier')
plt.show()
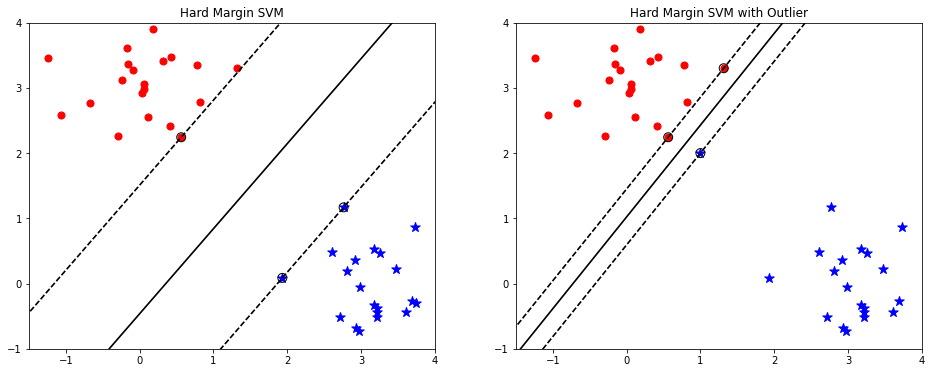
Hình 3: Hình bên trái là phân loại đường biên cứng (Hard margin SVM) đối với tập dữ liệu thông thường. Hình bên phải là phân loại đường biên cứng đối với dữ liệu chứa điểm ngoại lai (là điểm hình sao được khoanh tròn). Phương pháp phân loại đường biên cứng buộc phải phân loại đúng mọi điểm dữ liệu, bao gồm cả điểm ngoại lai. Điều này khiến cho đường biên phân chia bị thu hẹp lại. Khi đó qui luật phân chia sẽ không còn giữ được yếu tố tổng quát và dẫn tới hiện tượng quá khớp (overfitting). Kết quả dự báo trên tập kiểm tra khi đó sẽ kém hơn so với tập huấn luyện.
Để khắc phục hạn chế của phân loại đường biên cứng, kỹ thuật phân loại đường biên mềm (Sorf Margin Classification) chấp nhận đánh đổi để mở rộng lề và cho phép phân loại sai các điểm ngoại lai. Cụ thể hơn, thuật toán sẽ chấp nhận một số điểm bị rơi vào vùng của lề (vùng nằm giữa hai đường nét đứt, vùng này còn được gọi là vùng không an toàn) nhưng trái lại, chi phí cơ hội của sự đánh đổi đó là độ rộng lề lớn hơn. Đường biên phân chia được tạo ra từ kỹ thuật này thường nắm được tính tổng quát và hạn chế hiện tượng quá khớp.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from sklearn import svm
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
# fit the modelf
for i, (name, penalty) in enumerate([('hard margin', 100), ('soft margin', 0.05)]):
clf = svm.SVC(kernel='linear', C=penalty)
clf.fit(X, y)
# get the separating hyperplane
w = clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-5, 5)
yy = a * xx - (clf.intercept_[0]) / w[1]
# plot the parallels to the separating hyperplane that pass through the
# support vectors (margin away from hyperplane in direction
# perpendicular to hyperplane). This is sqrt(1+a^2) away vertically in
# 2-d.
margin = 1 / np.sqrt(np.sum(clf.coef_ ** 2))
yy_down = yy - np.sqrt(1 + a ** 2) * margin
yy_up = yy + np.sqrt(1 + a ** 2) * margin
# plot the line, the points, and the nearest vectors to the plane
ax[i].plot(xx, yy, 'k-')
ax[i].plot(xx, yy_down, 'k--')
ax[i].plot(xx, yy_up, 'k--')
ax[i].scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80,
facecolors='none', zorder=10, edgecolors='k',
cmap=cm.get_cmap('RdBu'))
ax[i].scatter(X[idx_cls_0, 0], X[idx_cls_0, 1], c='red', marker='o', s=50)
ax[i].scatter(X[idx_cls_1, 0], X[idx_cls_1, 1], c='blue', marker='*', s=100)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
x_min = -1.5
x_max = 4
y_min = -1
y_max = 4
# Put the result into a contour plot
ax[i].contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
ax[i].set_xlim(x_min, x_max)
ax[i].set_ylim(y_min, y_max)
if i == 0:
ax[i].set_title('Hard Margin SVM, C={}'.format(penalty))
else:
ax[i].set_title('Soft Margin SVM, C={}'.format(penalty))
plt.show()
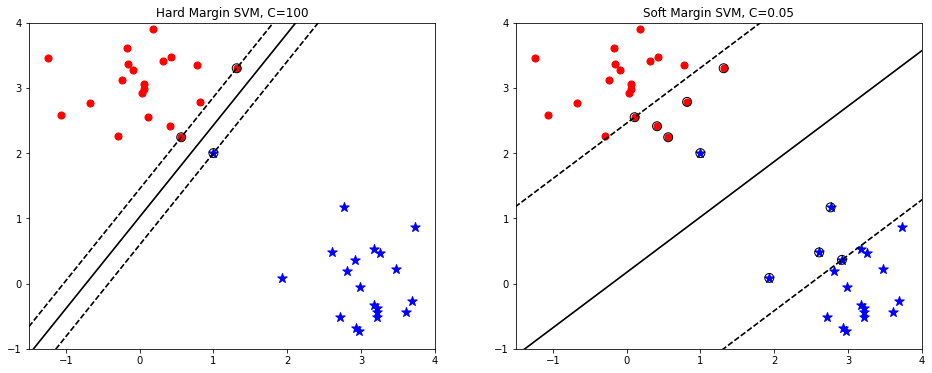
Hình 4: Phân loại biên cứng (bên trái) và phân loại biên mềm (bên phải) trong SVM. Chúng ta nhận thấy đối với đường biên mềm thì SVM chấp nhận một số điểm rơi vào vùng không an toàn để nhằm tạo ra một đường biên phân chia tổng quát hơn. Trong khi phân loại theo đường biên cứng thì không chấp nhận những điểm dữ liệu bị lấn sang vùng không an toàn.
7.4.2. Suy xét lại hàm chi phí cho phân loại đường biên mềm SVM¶
Ý tưởng của phân loại đường biên mềm là mở rộng lề và chấp nhận hi sinh một số điểm bị rơi vào vùng không an toàn để tạo ra một đường biên phân chia tổng quát hơn. Nhưng chúng ta không thể mở rộng lề ra vô cùng vì như vậy có nhiều điểm bị rơi vào vùng không an toàn hơn và dẫn tới sự hi sinh là quá lớn. Quá trình mở rộng lề sẽ bị kìm hãm sao cho đối với những điểm bị rơi vào vùng không an toàn thì tổng khoảng cách của chúng tới mép của lề về phía mặt phẳng của nhãn ground truth của chúng là nhỏ nhất. Khoảng cách này được thể hiện qua biến slack (ký hiệu \(\xi_n\)):

Hình 5: Khoảng cách từ một điểm tới mép của lề. Mặt dương bên trái là các điểm dấu x và bên phải là các điểm hình vuông. Xét 3 trường hợp của các điểm dấu x thuộc mặt dương. Điểm \(Z_1\) được phân về đúng mặt phân chia và nằm ngoài đường biên nên không bị phạt, điểm này có khoảng cách \(\xi_1=0\). Điểm \(Z_2\) tương ứng với \(\xi_2 > 1\), đây là những điểm vượt qua đường biên và bị phân loại sai. Điểm này có khoảng cách tới mép của lề như thể hiện trên hình là \(\xi_2 = \mathbf{w}^{\intercal}\mathbf{x}+b-1\). Điểm \(Z_3\) tương ứng với \(0 \leq \xi_3 \leq 1\), đây là những điểm chưa vượt qua đường biên sang phía bên kia. Do đó dù rơi vào vùng không an toàn nhưng vẫn được phân loại đúng nhãn. Khoảng cách của chúng tới mép của lề \(\xi_3 = 1-\mathbf{w}^{\intercal}\mathbf{x}-b\). Một cách tổng quát, nếu một điểm rơi vào vùng không an toàn thì khoảng cách xâm lấn của chúng là \(\xi_n = |b+\mathbf{w}^{\intercal}\mathbf{x}_i-y_i|\).
Bài tập: Chứng minh công thức khoảng cách xâm lấn \(\xi_n = |b+\mathbf{w}^{\intercal}\mathbf{x}_i-y_i|\) cho cả hai trường hợp \(y_i = 1\) và \(y_i = -1\).
Trong hàm mất mát tồn tại sự đánh đổi giữa sự hi sinh các điểm rơi vào vùng không an toàn và sự mở rộng của lề. Nếu muốn hi sinh ít điểm bị rơi vào vùng không an toàn hơn thì chúng ta cần lề phải hẹp hơn. Nhưng lề hẹp đồng nghĩa với mức độ khái quát của đường biên phân chia thấp như sự so so sánh đường biên cứng và mềm đã phân tích ở hình 2. Như vậy hàm mất mát là sự dung hoà giữa hai yếu tố tối thiểu hoá sự hi sinh các điểm và tối đa hoá khoảng cách:
Ràng buộc \(y_i(b+\mathbf{w}^{\intercal}\mathbf{x}_i) + \xi_i - 1 \geq 0 \leftrightarrow \xi_i \geq 1-y_i(b+\mathbf{w}^{\intercal}\mathbf{x}_i)\) có ý nghĩa rằng chúng ta chỉ cho phép các điểm bị lấn sang vùng không an toàn một ngưỡng tối đa \(\xi_i\). Ngoài ra trong bài toán tối ưu cần có thêm điều kiện ràng buộc \(\xi_i \geq 0\).
Hệ số \(C\) là một hệ số rất quan trọng thể hiện tỷ lệ đánh đối giữa sự mở rộng lề và và sự hi sinh. Một hệ số \(C\) lớn thì ảnh hường của \(||\mathbf{w}||_2^2\) sẽ không đáng kể lên giá trị của hàm mất mát. Giá trị của hàm mất mát chủ yếu đến từ tổng khoảng cách xâm lấn. Tối thiểu hàm mất mát đồng nghĩa với cần hạn chế bớt mức độ xâm lấn. Điều này dẫn tới độ rộng lề nhỏ hơn. Trong trường hợp tập dữ liệu là phân tuyến thì tồn tại một đường biên phân chia đúng mọi điểm dữ liệu. Như vậy \(\sum_{i=1}^N \xi_i = 0\) và ta thu được bài toán phân loại đường biên cứng (hard margin SVM).
Trái lại trường hợp \(C\) nhỏ dẫn tới \(||\mathbf{w}||_{2}^{2}\) nhỏ. Do đó độ rộng lề là lớn hơn. Điều đó đồng nghĩa với mức độ xâm lấn cũng lớn theo. Sẽ tồn tại một số điểm xâm lấn tương ứng với \(\xi_i > 0\) và trường hợp này tương ứng với bài toán phân loại đường biên mềm (soft margin SVM).
Bài toán tối ưu \((9)\) là một bài toán tối ưu QP và có thể giải thông qua hệ điều kiện KKT. Bài toán này có hàm đối ngẫu Lagrange:
Trong đó \(\lambda_i, \nu_i > 0, ~~ \forall i=\overline{1,N}\)
Điều kiện cần của cực trị theo đạo hàm bậc nhất của hàm Lagrange:
Đẳng thức \((10)\) và \((11)\) cho thấy chúng ta có thể suy ra các hệ số của phương trình đường biên thông qua những điểm có \(\lambda_i > 0\). Đây là những điểm nằm trên đường biên hoặc những điểm bị lấn vào lề.
Từ đẳng thức \((12)\) ta suy ra \(\nu_i = C-\lambda_i \geq 0\). Như vậy trong mọi trường hợp thì \(\lambda_i \leq C\).
Theo điều kiện complementary slackness của tiêu chuẩn KKT thì \(\lambda_i(1-\xi_i-y_i(\mathbf{w}^{\intercal}\mathbf{x}_i+b)) = 0\) và \(\nu_i\xi_i = 0\).
Trong trường hợp \(\lambda_i = 0\) thì \(\nu_i = C-\lambda_i = C > 0\). Như vậy để \(\nu_i\xi_i = 0\) thì \(\xi_i = 0\). Các điểm dữ liệu nằm trong vùng an toàn và không bị phạt.
Trong trường hợp \(0 < \lambda_i \leq C\) thì \(\nu_i = C - \lambda_i> 0\). Để \(\nu_i \xi_i = 0\) thì \(\xi_i = 0\). Mặt khác \(\lambda_i(1-\xi_i-y_i(\mathbf{w}^{\intercal}\mathbf{x}_i+b)) = 0 \leftrightarrow 1-\xi_i-y_i(\mathbf{w}^{\intercal}\mathbf{x}_i+b) = 0\). Thế \(\xi_i = 0\) ta thu được: \(1-y_i(\mathbf{w}^{\intercal}\mathbf{x}_i+b) = 0\). Đây là những điểm trong tập hỗ trợ giúp tạo thành đường biên phân chia.
Trong trường hợp \(\lambda_i = C\) thì \(\nu_i = C-\lambda_i = 0\). Như vậy giá trị \(\xi_i\) không nhất thiết phải bằng 0. Có thể tồn tại \(\xi_i > 0\) tương ứng với những điểm bị hi sinh.
Khi tiến hành tinh chỉnh mô hình, chúng ta quan tâm nhiều tới hệ số \(C\) vì nó ảnh hưởng trực tiếp tới hình dạng của đường biên và kiểm soát hiện tượng quá khớp.
Trong python để phân loại đường biên mềm thì chúng ta có thể sử dụng module sklearn.svm.SVC hoặc sklearn.svm.LinearSVC thông qua việc thiết lập đối số \(C\) thấp. Ở ví dụ hình 2 bạn cũng có thể thấy với Soft Margin SVM thì chúng ta để \(C=0.05\)
Ngoài ra LinearSVC cũng tương ứng với SVC với cấu hình kernel='linear' (tức là sử dụng kernel tuyến tính mà ta sẽ tìm hiểu bên dưới), module LinearSVC có tốc độ nhanh hơn so với SVC nên được khuyến nghị hồi qui với những tập dữ liệu lớn. Khi huấn luyện với bộ dữ liệu kích thước nhỏ (khoảng vài ngàn quan sát) thì có thể sử dụng SVC. Ưu điểm của SVC đó là chúng ta được phép lựa chọn đa dạng các phép biến đổi kernel. Trong khi LinearSVC là phương pháp dựa trên kernel linear. Trong LinearSVC cho phép chúng ta lựa chọn được loại hàm điều chuẩn thông qua đối số penalty và dạng của hàm mất mát thông qua đối số loss.
Tiếp theo chúng ta sẽ cùng tìm hiểu về tạo lập đặc trưng (feature engineering) trong SVM.
7.5. Kỹ thuật tạo đặc trưng¶
Trong thuật toán phân loại đường biên mềm SVM chúng ta sẽ quyết định nhãn cho một điểm dữ liệu dựa vào đường biên phân loại như sau:
Đường biên phân chia \(b + \mathbf{w}^{\intercal}\mathbf{x}_i\) sẽ là một đường thẳng trong không gian hai chiều và trong không gian 3 chiều đường biên này là một mặt phẳng (plane). Trong không gian nhiều hơn 3 chiều thì chúng ta gọi đường biên phân chia của SVM là một siêu phẳng (hyperplane). Hình dạng của những đường biên phân chia tuyến tính này là tương đối đơn giản nên để gia tăng hiệu quả của mô hình SVM thì chúng ta sẽ sử dụng các hàm biến đổi phi tuyến trên các biến đầu vào.
Một cách khái quát, giả định các hàm \(\varphi_1(.), \varphi_2(.), \dots , \varphi_n(.)\) là các hàm biến đổi phi tuyến (non-linear transformation function). Khi đó phương trình đường biên sẽ được chuyển sang phương trình của hàm biến đổi phi tuyến như sau:
Những biến đổi phi tuyến giúp chúng ta tạo ra được những đường biên phân loại phức tạp hơn và giúp cải thiện độ chính xác của mô hình. Có một số dạng hàm biến đổi phi tuyến là khá tường minh và dễ áp dụng như hàm đa thức (polynormial) và hàm Gaussian RBF (sẽ tìm hiểu bên dưới).
7.5.1. Đặc trưng đa thức (Polynormial Features)¶
Trong hầu hết các bài toán machine learning, khi muốn gia tăng độ chính xác cho mô hình thì chúng ta thường sử dụng kỹ thuật tạo lập đặc trưng đa thức (Polynormial Features). Kỹ thuật này sẽ thêm những biến bậc cao (chẳng hạn như \(x_1^2, x_1^3\)) và biến tích chéo (chẳng hạn \(x_1 x_2, x_1^2 x_2\)) vào mô hình để gia tăng khả năng biểu diễn cho mô hình phân loại. Kỹ thuật này đã được giới thiệu và áp dụng trong các mô hình hồi qui tuyến tính, hồi qui Logistic ở những chương trước.
7.5.2. Đặc trưng tương đồng Gaussian RBF¶
Bên cạnh phương pháp tạo lập đặc trưng đa thức (Polynormial Features) chúng ta còn sử dụng một phương pháp tạo lập đặc trưng tương đồng dựa trên hàm Gaussian RBF. Trên phân phối của tập dữ liệu chúng ta xác định một tập hợp các điểm landmarks. Landmarks ở đây được hiểu như là những điểm tiêu biểu đại diện cho các nhãn.
Một hàm độ đo Gaussian RBF (RBF là viết tắt của radial basis function) về bản chất là khoảng cách hoặc mức độ tương đồng giữa một điểm dữ liệu \(\mathbf{x}\) bất kỳ với một điểm landmark \(l\) có dạng như sau:
Trong đó \(\gamma\) là hằng số và \(||\mathbf{x}||_2\) là chuẩn bậc hai của \(\mathbf{x}\).
Đây là một hàm có phân phối đồng dạng với phân phối chuẩn nên hình dạng của chúng là một hình quả chuông đối xứng qua điểm landmark.
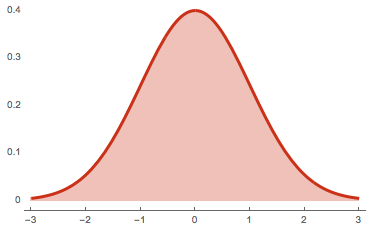
Giá trị của \(\varphi(\mathbf{x}, l)\) sẽ tiến gần tới 1 trong trường hợp \(\mathbf{x}\) và \(l\) gần nhau và trường hợp những điểm này là cách xa nhau thì giá trị \(\varphi(\mathbf{x}, l)\) sẽ tiến dần tới 0.
Sau khi đưa thêm các đặc trưng Gaussian RBF vào mô hình thì các điểm phân phối gần landmark có giá trị kernel gần 1 và tách biệt so với các điểm nằm cách xa landmark có giá trị gần 0. Chúng ta sẽ thấy rõ sự tách biệt trên không gian chiếu.

Hình 6: Chẳng hạn trong hình minh hoạ trên chúng ta có hai điểm landmark là \(l_1\) và \(l_2\) tạo thành một hình dạng phân phối đặc trưng cho một lớp (phân phối được bao quanh bởi đường nét đứt). Điểm \(\mathbf{x}_1\) gần \(l_1\) và \(\mathbf{x}_2\) nằm gần \(l_2\). Khi thực hiện phép chiếu dựa trên biến đổi Gaussian RBF thì toạ độ điểm \(\mathbf{x}\) sẽ được ánh xạ thành:
Thể hiện trên hình bên phải là 3 điểm ảnh tương ứng với \(\mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3\) của hình bên trái. Ta nhận thấy \(\mathbf{x}_1\) do gần \(l_1\) hơn nên có \(f_1\) cao và \(f_2\) thấp; tương tự như vậy \(\mathbf{x}_2\) gần \(l_2\) hơn nên có \(f_2\) cao, \(f_1\) thấp. \(\mathbf{x}_3\) thì cách xa cả hai điểm landmarks này nên có toạ độ sát điểm \((0, 0)\). Trên không gian chiếu ta dễ dàng phân biệt được ảnh của các điểm này bằng một đường biên nét đứt.
7.6. Kernel trong SVM¶
Sử dụng các phương pháp tạo lập đặc trưng thường mang lại hiệu quả. Tuy nhiên chúng có một số hạn chế đó là chúng ta phải thêm một lượng rất lớn các đặc trưng cho từng quan sát và dẫn tới chi phí tính toán gia tăng một cách đáng kể. Chẳng hạn nếu sử dụng hàm đa thức với bậc là 3 trên \(n\) biến thì số lượng biến bậc 3 được sinh ra có thể lên tới \(C_{n}^{1}+2*C_{n}^{2} + C_{n}^{3}\), đây là một giá trị rất lớn và gây lãng phí về chi phí tính toán. Trong SVM có một kỹ thuật giúp cho vẫn có thể áp dụng các biến đổi đặc trưng trên biến đầu vào mà không cần phải tính toán các đặc trưng sau biến đổi mà ta sẽ tìm hiểu bên dưới.
Ở mục 7.2.5 chúng ta biết rằng nhãn của một dự báo có thể được tính trên các điểm thuộc tập hỗ trợ.
Trong trường hợp biến đổi phi tuyến thì phương trình đường biên trở thành:
Để tính toán ra hàm \(\varphi()\) là khá khó khăn vì có một số trường hợp hàm biến đổi phi tuyến \(\varphi()\) tồn tại dưới một dạng tiềm ẩn (implicit function). Tức là chúng ta không thể tìm được trực tiếp dạng hàm mà chỉ biết được chúng tồn tại. Thay vì phải tính hàm \(\varphi()\) thì chúng ta sẽ tìm cách tính hàm \(\phi(\mathbf{x}_j, \mathbf{x}_i)\) sẽ đơn giản hơn rất nhiều. Từ đó hình thành nên một kĩ thuật rất quan trọng trong SVM dựa trên những khám phá về hàm hạt nhân (kernel function) \(\phi(\mathbf{x}_j, \mathbf{x}_i)\) đó là kỹ thuật kernel SVM.
Tiếp theo chúng ta sẽ tìm hiểu về kernel SVM.
7.6.1. Khái niệm hàm kernel (Kernel function) và không gian Hilbert¶
Không gian tích vô hướng (inner product) giữa các véc tơ còn được gọi là không gian Hilbert \(\langle \mathbf{x}, \mathbf{y} \rangle : \chi \times \chi \mapsto \mathcal{H}\)
Trong đó ký hiệu \(\langle \mathbf{x}, \mathbf{y} \rangle\) là tích vô hướng giữa hai véc tơ. \(\chi \times \chi \mapsto \mathcal{H}\) thể hiện rằng đây là một hàm có miền xác định là hai véc tơ trong không gian véc tơ \(\chi\) và được ánh xạ tới một điểm trong không gian Hilbert \(\mathcal{H}\). Lưu ý không gian Hilbert không chỉ xác định trong miền số thực mà còn xác định trong miền số phức. Không gian Hilbert sẽ thoả mãn một số tính chất trên miền số thực như:
1-. Tính chất hoán vị:
2-. Tính chất tuyến tính:
Với \(a, b\) là những hằng số. 3-. Tích vô hướng với chính véc tơ đó là một véc tơ bán xác định dương (semi - positive define):
Hàm kernel là một khái niệm có sự liên kết chặt chẽ và gần gũi với không gian Hilbert mà ở đó chúng ta không trực tiếp tính tích vô hướng giữa hai véc tơ mà thay vào đó ánh xạ hai véc tơ lên một không gian bản đồ đặc trưng (feature map) và sử dụng không gian bản đồ đặc trưng này như là đầu vào để ánh xạ lên không gian Hilbert.
Lưu ý: Hàm kernel giữa hai véc tơ \(\mathbf{x}, \mathbf{y}\) trong cuốn sách này được ký hiệu là \(\phi{}(\mathbf{x}, \mathbf{y})\). Hầu hết các tài liệu khác kí hiệu là \(K(\mathbf{x}, \mathbf{y})\) hoặc \(k(\mathbf{x}, \mathbf{y})\) nhưng bản thân tôi nhận thấy dùng chữ cái \(K\) hoặc \(k\) thì dễ bị nhầm với ma trận hoặc số vô hướng nên thay bằng hàm \(\phi()\).
Hàm đặc trưng (feature function) có thể là một hàm tiềm ẩn (implicit function) không thể biết định dạng cụ thể hoặc là một hàm hiện (explicit function) có thể biết định dạng. Như vậy về bản chất thì kernel function chính là một hàm: \(\phi(\mathbf{x}, \mathbf{y}) = \langle \varphi(\mathbf{x}), \varphi(\mathbf{y}) \rangle : \varphi(\chi) \times \varphi(\chi) \mapsto \mathcal{H}\).
Trong dó hàm đặc trưng chính là \(\varphi(\mathbf{x})\).
Khi sử dụng hàm kernel thông thường chúng ta sẽ tìm một phép biểu diễn véc tơ \(\mathbf{x}\) trong một không gian thấp chiều (low-dimensional space) sang một không gian cao chiều (high-dimensional space). Những thủ thuật biến đổi từ không gian thấp chiều sang không gian cao chiều thông qua hàm kernel được gọi là những mẹo kernel (kernel trick). Sử dụng kernel mang lại cho chúng ta hai lợi ích chính. Đó là chúng ta có thể tính được tích vô hướng giữa hai hàm đặc trưng mà không nhất thiết phải tìm ra biểu diễn của \(\mathbf{x}\) khi được ánh xạ sang không gian cao chiều. Vì hàm đặc trưng có số chiều thường rất lớn nên tiết kiệm được chi phí tính toán nếu biết trước được định dạng của hàm kernel.
7.6.2. Định lý merce về kernel¶
Như chúng ta đã phân tích, sử dụng các hàm biến đổi phi tuyến thì thường dẫn tới sự lãng phí về chi phí tính toán. Trong khi để dự báo nhãn thì chúng ta chỉ cần sử dụng hàm kernel là đủ. Như vậy điểm mấu chốt để giảm bớt chi phí tính toán đó là chúng ta phải tìm ra được hàm kernel phù hợp.
Theo định lý merce thì hàm \(\phi(\mathbf{x},\mathbf{y})\) cần thoả mãn một số điều kiện để trở thành một hàm kernel. Trong đó một điều kiện quan trọng là \(\phi()\) phải là một hàm liên tục và đối xứng. Tức là \(\phi(\mathbf{x},\mathbf{y}) = \phi(\mathbf{y},\mathbf{x})\). Tính chất này là để đảm bảo tồn tại một hàm \(\varphi\) ánh xạ các véc tơ \(\mathbf{x}\) và \(\mathbf{y}\) lên không gian cao chiều sao cho tích vô hướng: \(\phi(\mathbf{x},\mathbf{y}) = \varphi(\mathbf{x})^{\intercal} \varphi(\mathbf{y})\).
Lưu ý rằng hầu hết mọi hàm kernel đều thoả mãn mọi điều kiện merce nhưng vẫn có một số hàm kernel không thoả mãn vẫn hoạt động khá hiệu quả.
Hàm \(\varphi(\mathbf{x})\) ở đây là một véc tơ biểu diễn véc tơ \(\mathbf{x}\) trong không gian cao chiều mới. Giả định chúng ta muốn áp dụng một hàm kernel đa thức bậc 2 dạng \(\phi(\mathbf{x}, \mathbf{y}) = (\mathbf{x}^{\intercal}\mathbf{y})^2\) thì \(\varphi\) có thể là hàm \(\varphi(\mathbf{x}) = [x_1^2, \sqrt{2 x_1 x_2}, x_2^2]^{\intercal}\). Trong đó \(\mathbf{x} = [x_1, x_2]\) và \(\mathbf{y} = [y_1, y_2]\). Thật vậy:
Như vậy từ không gian 2 chiều, các véc tơ đã được biến đổi sang không gian 3 chiều. Trong machine learning có một số hàm kernel được sử dụng khá phổ biến. Chúng ta sẽ tìm hiểu những hàm kernel này bên dưới.
7.6.3. Các kernel khác cho SVM¶
Đây là những hàm kernel phổ biến đã được tích hợp bên trong package sklearn.
Kernel RBF: Kernel RBF dựa trên hàm Gaussian RBF. Hàm biến đổi phi tuyến của kernel này là hàm ẩn và tương đương với một đa thức với bậc vô hạn.
Kernel tuyến tính (linear): Đây là tích vô hướng giữa hai véc tơ.
Kernel đa thức (poly): Tạo ra một đa thức bậc cao kết hợp giữa hai véc tơ.
Kernel Sigmoid: Dựa trên kernel về đa thức, chúng ta đưa chuyển tiếp qua hàm tanh. Hàm tanh có thể biểu diễn theo hàm sigmoid nên đây được gọi là kernel Sigmoid.
Trong quá trình huấn luyện SVM chúng ta cần thử với những kernel khác nhau để tìm ra một kernel hiệu quả. Ở mục 6 thực hành các bạn sẽ được làm quen với việc tuning kernel.
Chú ý đối với các từng kernel thì chúng ta lại có thể tuning các siêu tham số (hyperameter) của chúng. Chẳng hạn như trong kernel đa thức chúng ta có thể tuning đối với bậc \(d\) của đa thức và hệ số \(\gamma\). Những phần này sẽ được hướng dẫn chi tiết hơn ở mục 6.
7.6.4. Dự báo nhãn¶
Nhãn của một quan sát trong mô hình kernel SVM sẽ phụ thuộc vào giá trị độ lớn của đường biên:
Từ dòng thứ \(1\) sang dòng thứ \(2\) là giá trị \(\mathbf{w}\) được tính trực tiếp từ các điểm thuộc tập hỗ trợ. Công thức trên rất quan trọng vì một số biến đổi kernel chúng ta sẽ không dễ dàng tìm được hàm \(\varphi(\mathbf{x})\) một cách trực quan. Chẳng hạn như với kernel RBF sẽ trả về hàm \(\varphi(\mathbf{x})\) tương đương với một hàm đa thức bậc vô hạn dẫn tới việc tính toán \(h_{\mathbf{w}, b}(\varphi(\mathbf{x}_i))\) là không khả thi và tốn kém. Nhưng thông qua hàm kernel thì chúng ta vẫn có thể tính toán được giá trị của phương trình đường biên một cách dễ dàng.
7.7. Ví dụ về bài toán SVM¶
Tiếp theo chúng ta sẽ cùng sử dụng SVM để phân loại bộ dữ liệu iris.
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.model_selection import cross_val_score
from sklearn.metrics import accuracy_score
iris = datasets.load_iris()
X = iris["data"]
y = (iris["target"] == 2).astype(np.int8) # 1 if virginica, 0 else
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
svm_pl = Pipeline((
("scaler", StandardScaler()),
("linear_svc", SVC(C=1, kernel="linear", probability = True))
)
)
svm_pl.fit(X, y)
scores = cross_val_score(svm_pl, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
print('Mean Accuracy: {:.03f}, Standard Deviation Accuracy: {:.03f}'.format(np.mean(scores), np.std(scores)))
Mean Accuracy: 0.960, Standard Deviation Accuracy: 0.050
Dự báo cho một quan sát mới
# Dự báo nhãn
svm_pl.predict(np.array([[1.2, 3.3, 2.2, 4.5]]))
array([1], dtype=int8)
# Dự báo xác suất, chỉ được khi probability trong SVC() được set True.
svm_pl.predict_proba(np.array([[3.2, 3.0, 4.2, 4.5]]))
array([[3.0000009e-14, 1.0000000e+00]])
7.7.1. Bài toán SVM cho dữ liệu dạng phi tuyến¶
Mặc dù SVM có kết quả khá tốt cho bài toán phân loại nhưng có một số tình huống dữ liệu là phức tạp và yêu cầu chúng ta phải thực hiện các phép biến đổi phi tuyến đối với biến đầu vào để tạo thành những đường biên phức tạp hơn. Kỹ thuật chuẩn hoá đa thức (polynormial) được áp dụng để tạo ra những biến bậc cao sẽ hữu ích trong những tình huống này:
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
svm_ply_pl = Pipeline((
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("linear_svc", SVC(C=1, kernel="linear", probability = True))
)
)
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(svm_ply_pl, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
print('Mean Accuracy: {:.03f}, Standard Deviation Accuracy: {:.03f}'.format(np.mean(scores), np.std(scores)))
Mean Accuracy: 0.969, Standard Deviation Accuracy: 0.041
Như vậy sau khi áp dụng chuẩn hoá đa thức thì độ chính xác đã tăng lên từ 0.96 lên 0.969. Đây là một trong những kỹ thuật thường được áp dụng để giúp cải thiện độ chính xác cho SVM.
Trên thực thế thì kỹ thuật chuẩn hoá đa thức cũng tương tự như việc sử dụng kernel poly trong module SVC. Lưu ý rằng mặc dù kỹ thuật chuẩn hoá đa thức thường mang lại sự cải tiến đáng kể về độ chính xác cho mô hình nhưng số lượng biến mà nó tạo ra bao gồm những biến tích chéo (dạng \(x_1^p x_2^q\)) và biến bậc cao (dạng \(x_1^l\)) là rất lớn. Do đó sẽ dễ xảy ra hiện tượng quá khớp và đồng thời gia tăng chi phí huấn luyện và tính toán.
Tiếp theo ta sẽ thực hành tuning kernel trong SVM.
7.7.2. Sử dụng kernel SVM¶
Khi huấn luyện mô hình SVM chúng ta cần thử với nhiều kernels khác nhau để tìm ra kernel tốt nhất cho bộ dữ liệu huấn luyện. Các kernel phổ biến đó là: linear, poly, rbf, sigmoid như đã được giới thiệu ở mục 7.5.2.
Ngoài ra nếu mô hình gặp hiện tượng quá khớp thì chúng ta cần điều chỉnh giảm hệ số \(C\) của mô hình SVM để gia tăng ảnh hưởng của thành phần kiểm soát.
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
kernels = ['linear', 'poly', 'rbf', 'sigmoid']
cv = RepeatedStratifiedKFold(n_splits=5, n_repeats=3, random_state=1)
all_scores = []
# Đánh giá toàn bộ các mô hình trên tập K-Fold đã chia
for kernel in kernels:
svm_kn_pl = Pipeline((
("scaler", StandardScaler()),
("linear_svc", SVC(C=1, kernel=kernel, probability = True))
)
)
scores = cross_val_score(svm_kn_pl, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
all_scores.append((kernel, scores))
import matplotlib.pyplot as plt
# Draw bboxplot
plt.figure(figsize=(16, 8))
plt.boxplot([score[1] for score in all_scores])
plt.xlabel('Scale', fontsize=16)
plt.ylabel('cm', fontsize=16)
plt.xticks(np.arange(len(kernels))+1, kernels, rotation=45, fontsize=16)
plt.title("Scores Metrics", fontsize=18)
Text(0.5, 1.0, 'Scores Metrics')
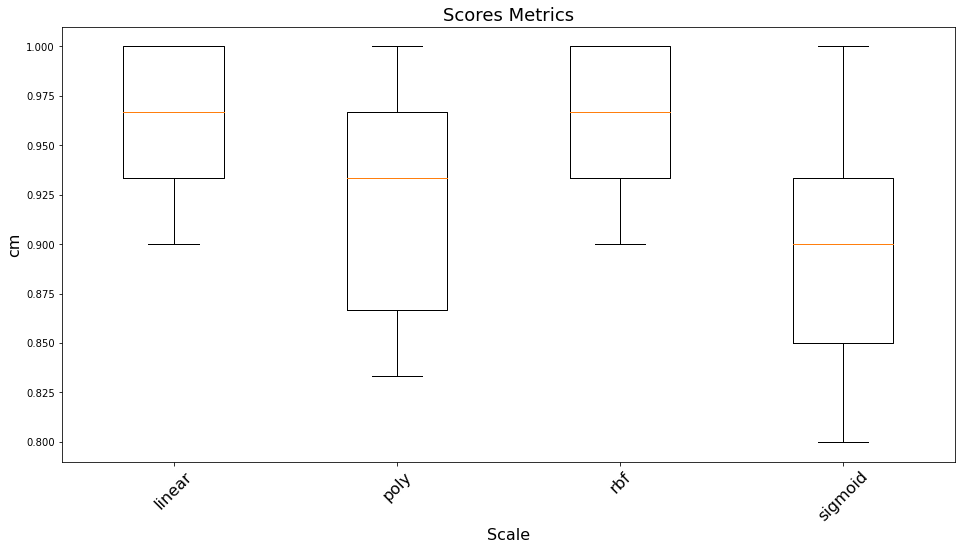
Như vậy ta có thể thấy các kernel hiệu quả chính là rbf và linear khi cùng có giá trị trung vị vào khoảng 0.97 và cao hơn mức trung bình của kernel kém nhất là Sigmoid là 0.07 điểm. Đây là một mức cải thiện khá đáng kể cho một bài toán phân loại nhị phân.
7.7.3. tuning siêu tham số cho một kernel¶
Đối với mỗi một dạng hàm kernel, căn cứ vào phương trình của chúng ta có thể xác định được những siêu tham số cần tuning.
Chẳng hạn như đối với danh sách các kernel được cung cấp ở mục 5.1 thì chúng ta có thể tuning các tham số như sau:
kernel tuyến tính: tham số C.
kernel đa thức: tham số \(C, \gamma, d\)
kernel RBF: tham số \(C, \gamma\).
kernel sigmoid: tham số \(C, \gamma, d\)
Công thức tổng quát của một mô hình SVC:
sklearn.svm.SVC(*,
C=1.0,
kernel='rbf',
degree=3,
gamma='scale',
coef0=0.0,
class_weight=None,
decision_function_shape='ovr',
random_state=None
)
Trong class SVC của sklearn thì hệ số \(\gamma\) tương ứng với đối số coef0, hệ số bậc đa thức \(d\) là đối số degree, trọng số \(C\) của hàm chi phí chính là đối số C và loại kernel là đối số kernel.
Ngoài ra trong trường hợp mẫu bị mất cân bằng nghiêm trọng thì chúng ta thiết lập class_weight để phạt nặng hơn những trường hợp mẫu thiểu số.
decision_function_shape là đối số cho phép chúng ta cấu hình kết quả xác suất dự báo trả về là theo phương pháp one-vs-rest hay one-vs-one. Nếu theo phương pháp one-vs-rest thì mô hình phân loại gồm \(C\) nhãn sẽ được chia thành \(C\) bài toán phân loại con, mỗi một bài toán tương ứng với một dự báo xác suất thuộc về nhãn \(i\). Còn đối với bài toán one-vs-one chúng ta sẽ tìm cách xây dựng \(C\times(C-1)\) mô hình phân loại cho một cặp nhãn \((i, j)\) bất kỳ. Đối với bài toán phân loại nhị phân thì decision_function_shape = ovr tương ứng với dự báo xác suất tương ứng với nhãn \((0, 1)\).
Bên dưới là một ví dụ mẫu về cách tuning tham số trên GridSearch đối với mô hình SVM.
from sklearn.model_selection import GridSearchCV
parameters = {
'clf__kernel':['linear', 'rbf', 'poly', 'sigmoid'], # Các dạng hàm kernel
'clf__C':[0.05, 1, 100], # Trọng số của phạt phân loại sai
'clf__coef0': [2, 4], # Tương ứng với tham số gamma của đa thức
'clf__degree': [1, 2, 3] # Bậc d của đa thức
}
pipeline = Pipeline(
steps=[("clf", SVC())]
)
gscv = GridSearchCV(pipeline, parameters, cv=5, n_jobs=12, scoring='accuracy', return_train_score=True, error_score=0, verbose=3)
gscv.fit(X, y)
Fitting 5 folds for each of 72 candidates, totalling 360 fits
GridSearchCV(cv=5, error_score=0, estimator=Pipeline(steps=[('clf', SVC())]),
n_jobs=12,
param_grid={'clf__C': [0.05, 1, 100], 'clf__coef0': [2, 4],
'clf__degree': [1, 2, 3],
'clf__kernel': ['linear', 'rbf', 'poly', 'sigmoid']},
return_train_score=True, scoring='accuracy', verbose=3)
7.8. Tổng kết¶
Như vậy qua chương này bạn đọc đã được giới thiệu những kiến thức cơ bản gồm:
Hàm mất mát trong SVM.
Khái niệm về đường biên và lề.
Bài toán phân loại SVM với đường biên mềm và đường biên cứng.
Các dạng bộ lọc trong SVM.
Phương pháp tuning tham số đối với mô hình SVM.
SVM làm một trong những thuật toán hoạt động khá hiệu quả trong lớp các bài toán phân loại và dự báo của học có giám sát. Nắm vững thuật toán này, bạn đọc sẽ có thêm công cụ để tạo ra những mô hình mạnh giúp giải quyết những vấn đề thực tế.
7.9. Bài tập¶
Hàm mất mát của SVM có dạng là một hàm có dạng như thế nào?
Phương trình đường biên của SVM được xác định như thế nào?
Dự báo nhãn của mô hình SVM sẽ căn cứ vào đâu?
Giả định mô hình hồi qui SVM đang gặp hiện tượng quá khớp. Làm thế nào để giảm thiểu hiện tượng quá khớp cho mô hình SVM?
Kernel trong SVM là gì? Kernel có tác dụng như thế nào đối với mô hình SVM?
Nêu các tiêu chuẩn để một hàm có thể trở thành một hàm kernel?
Có những dạng kernel chính nào trong SVM? Đặc điểm của chúng là gì?
Sử dụng hàm kernel có ưu điểm gì khi dự báo nhãn?
Kernel RBF có hàm biến đổi phi tuyến là một hàm như thế nào?
Khi huấn luyện một mô hình SVM thì chúng ta cần tinh chỉnh những siêu tham số nào là chủ yếu?
