.ipynb .md .pdf

repository open issue suggest edit

Binder

Contents

6.1. Phương pháp chuyên gia và mô hình

Để đánh giá rủi ro tín dụng chúng ta có thể áp dụng phương pháp chuyên gia hoặc sử dụng mô hình thống kê. Mỗi phương pháp đều có các ưu nhược điểm khác nhau. Tiếp theo chúng ta sẽ cùng nhau phân biệt hai phương pháp này:

Phương pháp chuyên gia: Như tên gọi của nó, phương pháp chuyên gia sẽ dựa trên ý kiến thẩm định của các chuyên gia về rủi ro đối với một khoản tín dụng. Rủi ro sẽ được căn cứ trên các thông tin chủ yếu đó là:

• Đặc điểm của chủ thể vay (character): Thẩm định danh tiếng, tính trung thực của người vay vốn.

• Vốn (capital): Thẩm định sự chênh lệch giữa tài sản và nguồn vốn của người cho vay. Tài sản chính là những giá trị mà ngân hàng có thể thu hồi khi người vay không trả được nợ. Nguồn vốn có thể là các chi phí mà người vay đang phải chi trả như chi tiêu gia đình, chi phí sinh hoạt, chi phí trả lãi từ các khoản vay khác,…. Sau khi trừ đi các chi phí chúng ta sẽ biết được giá trị khả dụng của người vay và liệu nó có đủ để bao quát lãi vay hay không?

• Tài sản đảm bảo (collateral): Sẽ có 2 loại hình thức cho vay được phân chia dựa trên tài sản đảm bảo đó là vay thế chấp (có tài sản đảm bảo) và vay tín chấp (không có tài sản đảm bảo). Rủi ro của 2 hình thức cho vay này là khác biệt nhau nên lãi suất và hạn mức của chúng cũng sẽ khác biệt để đảm bảo dung hòa giữa lợi nhuận và rủi ro đối với ngân hàng. Đối với vay thế chấp ngân hàng sẽ phải định giá chính xác giá trị của các tài sản thế chấp. Gía trị các tài sản này sẽ quyết định hạn mức tín dụng mà ngân hàng sẽ cấp cho người vay. Rủi ro đối với các khoản vay thế chấp là thấp hơn tín chấp vì trong trường hợp khách hàng không có khả năng thanh toán, ngân hàng được quyền thu hồi tài sản đảm bảo.

• Khả năng trả nợ (capacity): Là các thông tin liên quan trực tiếp đến khả năng tài chính của người vay đó là: nghề nghiệp, mức thu nhập, trạng thái hôn nhân, số người phụ thuộc,….

• Điều kiện (condition): Đánh giá sơ bộ trạng thái của người vay có tham chiếu tới điều kiện thị trường, bối cảnh tài chính, áp lực cạnh tranh, mục đích sử dụng vốn,…. Chẳng hạn người vay là hộ dân trồng cafe nhưng năm vừa qua thị trường cafe giảm giá mạnh. Do đó sẽ khiến lợi nhuận và khả năng thanh toán của người vay xuống thấp hơn dự kiến.

Phương pháp chuyên gia là phương pháp thủ công vì nó dựa trên kinh nghiệm của con người. Do đó quá trình thẩm định sẽ tốn kém về thời gian. Đồng thời ý kiến đánh giá cũng không nhất quán giữa các chuyên gia. Do đó một phương pháp khác được khuyến nghị phát triển ở hội nghị basel nhằm đưa ra các đánh giá nhanh chóng và nhất quán hơn. Đó chính là phương pháp mô hình.

Phương pháp mô hình: Phương pháp mô hình sẽ dựa trên điểm số được lượng hóa từ mô hình học máy. Phương pháp này có nhiều điểm tối ưu hơn so với phương pháp chuyên gia:

• Những mô hình đưa ra kết quả dường như là ngay lập tức. Do đó thời gian thẩm định hồ sơ nhanh chóng và rất phù hợp với các nền tảng cho vay online.

• Năng suất thẩm định từ mô hình cao hơn rất nhiều so với các chuyên gia. Một môt hình có thể giải quyết số lượng hồ sơ bằng khối lượng công việc của hàng trăm chuyên gia.

• Giảm thiểu chi phí lao động khi không phải chi trả lương cho các chuyên gia thẩm định.

• Kết quả đánh giá hồ sơ là rất nhất quán dựa trên điểm số tín nhiệm là duy nhất, trong khi đó các chuyên gia có thể đưa ra kết quả đánh giá khác nhau dựa trên cảm quan của họ về rủi ro. Khi xảy ra bất đồng ý kiến, sẽ cần hội đồng chuyên gia đánh giá lại hồ sơ và khá tốn thời gian để hoàn thành thẩm định.

• Mô hình sẽ xem xét toàn diện các biến số đầu vào và thậm chí có thể gia tăng số lượng biến tùy ý mà không ảnh hưởng tới thời gian dự báo. Trong khi phương pháp chuyên gia sẽ chịu hạn chế bởi khả năng của con người là có hạn. Việc đánh giá hồ sơ đôi khi chỉ được nhận định trên một số biến chính.

Chính vì những lợi thế đó, phương pháp mô hình đang dần thay thế phương pháp chuyên gia và trở thành phương pháp thẩm định chủ yếu tại các ngân hàng.

6.2. Xây dựng mô hình credit scorecard

Có nhiều thuật toán khác nhau được áp dụng để xây dựng mô hình scorecard. Trong bài này tôi sẽ chỉ giới thiệu mô hình thông dụng nhất đối với bài toán phân loại nợ xấu trong lớp các mô hình phân loại nhị phân, đó là hồi qui Logistic. Về hồi qui Logistic các bạn xem thêm tại 3.1. Logistic Regression để nắm rõ nội dung của phương pháp này. Quá trình hồi qui sẽ tiếp nhận các đặc trưng đầu vào đã được tiền xử lý theo phương pháp trọng số dấu hiệu, viết tắt là WOE, cụ thể sẽ được giới thiệu bên dưới. Cuối cùng đầu ra của mô hình là xác suất vỡ nợ (default probability) đánh giá khả năng vỡ nợ của một hồ sơ vay vốn. Xác suất càng cao là dấu hiệu cho thấy khả năng vỡ nợ càng lớn. Từ xác suất, thông qua các phép biến đổi để chuyển sang điểm số tín nhiệm (credit score) đại diện cho mức độ uy tín của khách hàng. Điểm số này bằng tổng các điểm số tương ứng với mỗi một đặc trưng của người dùng được tạo ra từ WOE. Bạn đọc sẽ nắm rõ hơn điều này ở phần trình bày bên dưới.

6.2.1. Weight of Evidence - WOE

WOE (weight of evidence) là một trong những kĩ thuật tạo đặc trưng (feature engineering) và lựa chọn đặc trưng (feature selection) khá hiệu quả, thường được áp dụng trong quá trình xây dựng mô hình scorecard. Phương pháp này sẽ xếp hạng các biến thành mạnh, trung bình, yếu, không tác động,… dựa trên điểm số đánh giá về sức mạnh dự báo nợ xấu. Tiêu chuẩn xếp hạng sẽ là chỉ số giá trị thông tin IV (information value) được tính toán từ phương pháp WOE. Đồng thời mô hình cũng tạo ra các đặc trưng cho mỗi biến. Giá trị này sẽ đo lường sự khác biệt trong phân phối giữa GOOD và BAD. Cụ thể như sau:

Phương pháp WOE sẽ có các kĩ thuật xử lý khác biệt đối với biến liên tục và biến phân loại:

• Trường hợp biến liên tục: WOE sẽ gán nhãn cho mỗi một quan sát theo nhãn giá trị bins mà nó thuộc về. Các bins sẽ là các khoảng liên tiếp được xác định từ biến liên tục sao cho số lượng quan sát ở mỗi bin là bằng nhau. Để xác định các bins thì ta cần xác định số lượng bins. Chúng ta có thể hình dung đầu mút của các khoảng bins chính là các quantile.

• Trường hợp biến phân loại: WOE có thể cân nhắc mỗi một nhóm là một bin hoặc có thể nhóm vài nhóm có số lượng quan sát ít vào một bin. Ngoài ra mức độ chênh lệch giữa phân phối GOOD/BAD được đo lường thông qua chỉ số WOE cũng có thể được sử dụng để nhận diện các nhóm có cùng tính chất phân loại. Nếu giá trị WOE của chúng càng gần nhau thì có thể chúng sẽ được nhóm vào một nhóm. Ngoài ra, trường hợp Null cũng có thể được coi là một nhóm riêng biệt nếu số lượng của nó là đáng kể hoặc nhóm vào các nhóm khác nếu nó là thiểu số.

Để hình dung cách tính WOE, tôi lấy ví dụ:

Độ tuổi của một khách hàng vay vốn rơi vào khoảng từ 20-60 tuổi. Ta sẽ phân chia độ tuổi này thành các bins sao cho số lượng quan sát của chúng là gần bằng nhau và thống kê số lượng hồ sơ good và bad trên từng bin đó. Sau cùng ta thu được một bảng như bên dưới:

Bảng 1: Bảng tính toán hệ số bằng chứng WOE và giá trị thông tin IV.

Các cột có ý nghĩa như sau:

• No observation: Số lượng các quan sát trong từng bins. Thường sẽ được chia bằng nhau giữa các bins để không có sự thiên lệch.

• No Good: Số lượng hồ sơ là nợ xấu ở mỗi bins. Chúng ta coi những hồ sơ vỡ nợ là Good vì Good không phải đại diện cho chất lượng của hồ sơ mà chỉ đơn thuần đánh dấu các hồ sơ nhãn là 1.

• No Bad: Số lượng hồ sơ không là nợ xấu ở mỗi bins. Nhãn của hồ sơ là 0.

• Good/Bad: Tỷ lệ hồ sơ Good/Bad ở mỗi bins.

• %Good: Phân phối của các hồ sơ good trên toàn bộ các bins. Tổng cột bằng 1.

• %Bad: Phân phối của các hồ sơ bad trên toàn bộ các bins. Tương tự như %Good cũng có tổng bằng 1.

• WOE (Weight of Evidence): Trọng số bằng chứng được sử dụng để đo lường sự khác biệt giữa tỷ lệ %Good và %Bad trên từng bin. Trọng số bằng chứng được tính toán bằng logarit của %Good/%Bad. Chẳng hạn tại bin 20-30 chúng ta biết được %Good = 0.313 và %Bad = 0.192, khi đó giá trị WOE tại bin này như sau:

\[\text{WOE}_{20-30} = \ln(\frac{\text{ %Good}}{\text{ %Bad}}) = \ln(\frac{0.313}{0.192}) = 0.491\]

Tính chất của WOE: Giá trị WOE tại một bin càng lớn là dấu hiệu chứng tỏ đặc trưng rất tốt trong việc nhận diện hồ sơ Good và trái lại nếu giá trị WOE càng nhỏ thì đặc trưng bin sẽ rất tốt trong việc nhận diện hồ sơ Bad. WOE > 1 thì phân phối của hồ sơ Good đang chiếm ưu thế hơn Bad và trái lại.

• IV (Information Value): Chỉ số giá trị thông tin, có tác dụng đánh giá một biến có sức mạnh trong việc phân loại nợ xấu hay không. Công thức tính IV:

\[\sum_{i=1}^{n}({\text{ %Good}_{i}-\text{ %Bad}_{i}).\text{WOE}_{i}}\]

Ta nhận thấy IV luôn nhận giá trị dương vì \(\text{WOE}_{i}\) và \((\text{ %Good}_{i}-\text{ %Bad}_{i})\) đồng biến. Gía trị IV sẽ cho ta biết mức độ chênh lệch của %Good và %Bad ở mỗi bin là nhiều hay ít. Nếu IV cao thì sự khác biệt trong phân phối giữa %Good và %Badsẽ lớn và biến hữu ích hơn trong việc phân loại hồ sơ và trái lại IV nhỏ thì biến ít hữu ích trong việc phân loại hồ sơ. Một số tài liệu cũng đưa ra tiêu chuẩn phân loại sức mạnh của biến theo giá trị IV như bên dưới:

• <= 0.02: Biến không có tác dụng trong việc phân loại hồ sơ Good/Bad.

• 0.02 - 0.1: yếu

• 0.1 - 0.3: trung bình

• 0.3 - 0.5: mạnh

• => 0.5: Biến rất mạnh, tuy nhiên trường hợp này cần được điều tra lại để tránh trường hợp biến có mối quan hệ trực tiếp để định nghĩa hồ sơ Good/Bad.

6.2.2. Ưu và nhược điểm của phương pháp WOE

Sở dĩ các mô hình scorecard lại ưa chuộng WOE bởi vì chúng có những ưu điểm đó là:

• WOE giúp biến đổi các biến đầu vào liên tục thành những biến có mối quan hệ đơn điệu (đồng biến hoặc nghịch biến) đối với biến mục tiêu. Thật vậy, giả sử thống kê cho thấy đối với độ tuổi của khách hàng trong các khoảng 20-30, 30-40, 40-50, 50+ thì tỷ lệ %GOOD/%BAD là [0.1, 0.5, 0.2, 0.3]. Như vậy AGE sẽ không có mối quan hệ đồng biến với tỷ lệ %GOOD/%BAD, tức là nó không có mối quan hệ đồng biến với biến mục tiêu. Trong khi nếu hồi qui giá trị gốc của AGE theo Logistic thì mối quan hệ với biến mục tiêu của AGE sẽ là đơn điệu (đơn điệu tăng hay giảm phụ thuộc vào dấu của hệ số hồi qui). Điều này là trái với thực tế. Do đó, phương pháp WOE giúp ta chia nhỏ các biến liên tục thành các khoảng biến mà giá trị của nó là đơn điệu với biến mục tiêu tuỳ thuộc vào dấu của WOE tương ứng với mỗi khoảng. Do đó các hệ số trong phương trình hồi qui Logistic sẽ giải thích được đúng thực tế mối quan hệ giữa biến đầu vào với biến mục tiêu.

• Phương pháp WOE giúp loại bỏ các outliers vì các biến có khoảng biến thiên lớn sẽ được nhóm về các nhóm bins. Gía trị của các quan sát outliers sẽ không còn khác biệt so với các những quan sát khác thuộc cùng nhóm vì chúng cùng được gán giá trị bằng trọng số WOE.

• Giá trị WOE phản ánh được ảnh hưởng của từng nhóm lên biến phụ thuộc. Vì giá trị WOE thể hiện chênh lệch về tỷ lệ giữa %GOOD/%BAD, đây là chỉ số ảnh hưởng trực tiếp đến xác suất vỡ nợ của khách hàng.

• Đối với các biến có nhiều nhóm nhỏ thì WOE sẽ nhóm chúng thành các nhóm lớn có hệ số WOE thể hiện thông tin chung cho toàn bộ nhóm.

Chính nhờ những lợi thế trên mà WOE đã được sử dụng phổ biến trong các mô hình credit scorecard.

Tuy nhiên phương pháp WOE cũng có những hạn chế nhất định đó là:

• Khi tính toán WOE, rất khó để biết phân chia bao nhiêu bins là phù hợp đối với biến liên tục. Việc gộp nhóm hoặc tách nhóm cũng được thực hiện thủ công dựa trên phân tích giá trị của WOE.

• Do các biến WOE là luôn đơn điệu với biến mục tiêu nên giữa các biến đầu vào luôn có sự tương quan (do cùng tương quan với biến mục tiêu). Điều này có thể dẫn đến nguy cơ đa cộng tuyến cao ảnh hưởng tới khả năng giải thích của hệ số hồi qui.

6.2.3. Tiêu chuẩn mô hình scorecard

Vì là một mô hình liên quan đến định lượng tín nhiệm khách hàng và ảnh hưởng đến quyết định cấp vốn nên khi phát triển một mô hình scorecard và cân nhắc ứng dụng mô hình đó vào thực tiễn, ngân hàng cần phải xem xét đến các khía cạnh rủi ro có thể phát sinh để đảm bảo việc áp dụng mang lại hiệu quả và hạn chế các rủi ro tiềm ẩn. Các tiêu chuẩn cần đạt được của một mô hình credit scorecard đó là:

• Khả năng diễn giải (Interpretability): Một mô hình có khả năng diễn giải tốt sẽ dễ dàng áp dụng vào thực tiễn hơn so với các mô hình có khả năng diễn giải kém. Chẳng hạn khi áp dụng 2 thuật toán khác nhau là hồi qui Logistic và mạng Nơ ron vào xây dựng một mô hình phân loại nợ xấu thì mạng nơ ron có thể mặc dù mang lại kết quả tốt hơn nhưng mô hình hồi qui Logistic vẫn được ưa chuộng hơn vì nó có khả năng giải thích được tác động của các đặc trưng lên điểm số cuối cùng.

• Độ chính xác kì vọng (Expectation Accuracy): Một mô hình trước khi đưa vào áp dụng cần phải đạt được một ngưỡng chính xác kì vọng. Ngưỡng chính xác này nên được thiết lập theo một thước đo phù hợp, chúng có thể là: độ chính xác (Accuracy), độ chuẩn xác (Precision), độ phủ (Recall), f1 score, AUC, Gini, Kappa giúp đánh giá bài toán phân loại. Thời điểm thiết lập kì vọng nên được tiến hành ở đầu dự án để tạo ra mục tiêu nhất quán trong suốt quá trình phát triển mô hình. Ngoài ra giá trị thiết lập nên được tham chiếu đến một số cơ sở thực tiễn chẳng hạn như: Khuyến nghị của các tổ chức tư vấn tài chính, độ chính xác mà một số ngân hàng khác đã đạt được trong cùng một thị trường, độ chính xác từ phương pháp chuyên gia,….

• Chi phí xây dựng (Cost): Để xây dựng một mô hình scorecard sẽ khá tốn kém về mặt chi phí và nguồn lực. Đội ngũ phát triển sẽ phải bỏ công sức thu thập dữ liệu, xử lý dữ liệu, huấn luyện mô hình. Ngoài ra việc sử dụng một số nguồn dữ liệu ngoài như dữ liệu lịch sử tín dụng từ cục tín dụng sẽ phải mất phí. Quá trình xây dựng mô hình cần phải tuân theo chuẩn basel nên có thể sẽ cần tới chi phí thuê tư vấn từ bên thứ ba. Sau khi xây dựng mô hình sẽ phát sinh thêm các chi phí về hậu kiểm, vận hành và đánh giá lại mô hình định kì. Do đó cần ước tính chúng trước khi xây dựng mô hình để dự án đạt hiệu quả lớn nhất.

Xây dựng mô hình scorecard là một quá trình lâu dài, từ khâu huấn luyện cho tới duy trì và vận hành. Đòi hỏi chúng ta phải thoả mãn các tiêu chuẩn chặt chẽ theo qui định của Basel. Trong khuôn khổ hạn hẹp, các nội dung liên quan tới tiêu chuẩn của Basel sẽ nằm ngoài bài viết này. Tiếp theo chúng ta sẽ cùng thực hành xây dựng một mô hình scorecard trên bộ dữ liệu hmeq.

6.2.4. Xây dựng model ScoreCard

Sau đây chúng ta sẽ cùng xây dựng một model scorecard từ bộ dữ liệu hmeq. Thông tin cụ thể về các biến trong bộ dữ liệu này như sau:

Bộ dữ liệu HMEQ bao gồm các đặc trưng thông tin nợ quá hạn của 5960 khoản vay mua nhà. Đây là những khoản vay mà người vay sử dụng vốn chủ sở hữu làm tài sản thế chấp cơ sở. Tập dữ liệu bao gồm những trường sau:

• BAD: 1 = Hồ sơ vay là vi phạm hoặc mất khả năng trả nợ; 0 = hồ sơ vay đã và đang trả nợ.

• LOAN: Số tiền yêu cầu cho vay.

• MORTDUE: Số tiền đến hạn của khoản thế chấp hiện có.

• VALUE: Giá trị tài sản hiện tại.

• REASON: DebtCon = nợ hợp nhất; HomeImp = cải thiện nhà.

• JOB: Thể loại nghề nghiệp.

• YOJ: Số năm kinh nghiệm trong nghề nghiệp hiện tại.

• DEROG: Số lượng báo cáo không tín nhiệm.

• DELINQ: Số hạn mức tín dụng quá hạn.

• CLAGE: Tuổi của hạn mức tín dụng cũ nhất tính theo tháng.

• NINQ: Số câu hỏi tín dụng gần đây.

• CLNO: Số lượng hạn mức tín dụng.

• DEBTINC: Tỷ lệ nợ trên thu nhập.

Có tổng cộng 12 biến đầu vào bao gồm cả biến numeric và biến category. Về cơ bản số lượng quan sát là đủ lớn để xây dựng mô hình credit scorecard. Tiếp theo chúng ta sẽ khảo sát dữ liệu.

6.2.4.1. Khảo sát dữ liệu

import pandas as pd

data = pd.read_csv('http://www.creditriskanalytics.net/uploads/1/9/5/1/19511601/hmeq.csv', header = 0, sep = ',')

Khảo sát dữ liệu

data.describe()

	BAD	LOAN	MORTDUE	VALUE	YOJ	DEROG	DELINQ	CLAGE	NINQ	CLNO	DEBTINC
count	5960.000000	5960.000000	5442.000000	5848.000000	5445.000000	5252.000000	5380.000000	5652.000000	5450.000000	5738.000000	4693.000000
mean	0.199497	18607.969799	73760.817200	101776.048741	8.922268	0.254570	0.449442	179.766275	1.186055	21.296096	33.779915
std	0.399656	11207.480417	44457.609458	57385.775334	7.573982	0.846047	1.127266	85.810092	1.728675	10.138933	8.601746
min	0.000000	1100.000000	2063.000000	8000.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.524499
25%	0.000000	11100.000000	46276.000000	66075.500000	3.000000	0.000000	0.000000	115.116702	0.000000	15.000000	29.140031
50%	0.000000	16300.000000	65019.000000	89235.500000	7.000000	0.000000	0.000000	173.466667	1.000000	20.000000	34.818262
75%	0.000000	23300.000000	91488.000000	119824.250000	13.000000	0.000000	0.000000	231.562278	2.000000	26.000000	39.003141
max	1.000000	89900.000000	399550.000000	855909.000000	41.000000	10.000000	15.000000	1168.233561	17.000000	71.000000	203.312149

mean của BAD chính là tỷ lệ số hợp đồng nợ xấu và chiếm 19.95%. Ta sẽ visualize phân phối của các biến để tìm hiểu phân phối của chúng.

import seaborn as sns
import matplotlib.pyplot as plt
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)

# Biểu đồ histogram
def _plot_hist_subplot(x, fieldname, bins = 10, use_kde = True):
  x = x.dropna()
  xlabel = '{} bins tickers'.format(fieldname)
  ylabel = 'Count obs in {} each bin'.format(fieldname)
  title = 'histogram plot of {} with {} bins'.format(fieldname, bins)
  ax = sns.distplot(x, bins = bins, kde = use_kde)
  ax.set_xlabel(xlabel)
  ax.set_ylabel(ylabel)
  ax.set_title(title)
  return ax

# Biểu đồ barchart
def _plot_barchart_subplot(x, fieldname):
  xlabel = 'Group of {}'.format(fieldname)
  ylabel = 'Count obs in {} each bin'.format(fieldname)
  title = 'Barchart plot of {}'.format(fieldname)
  x = x.fillna('Missing')
  df_summary = x.value_counts(dropna = False)
  y_values = df_summary.values
  x_index = df_summary.index
  ax = sns.barplot(x = x_index, y = y_values, order = x_index)
  # Tạo vòng for lấy tọa độ đỉnh trên cùng của biểu đồ và thêm label thông qua annotate.
  labels = list(set(x))
  for label, p in zip(y_values, ax.patches):
    ax.annotate(label, (p.get_x()+0.25, p.get_height()+0.15))
  plt.xlabel(xlabel)
  plt.ylabel(ylabel)
  plt.title(title)
  return ax

# Khởi tạo figure cho đồ thị (Kích thước W*H = 16x12) và cách nhau là 0.2 giữa các đồ thị
fig = plt.figure(figsize=(18, 16))
fig.subplots_adjust(hspace=0.5, wspace=0.2)
# Tạo vòng for check định dạng của biến và visualize
for i, (fieldname, dtype) in enumerate(zip(data.columns, data.dtypes.values)):
  if i <= 11:
    ax_i = fig.add_subplot(4, 3, i+1)
    if dtype in ['float64', 'int64']:
      ax_i = _plot_hist_subplot(data[fieldname], fieldname=fieldname)
    else:
      ax_i = _plot_barchart_subplot(data[fieldname], fieldname=fieldname)
      
fig.suptitle('Visualization all fields')
plt.show()

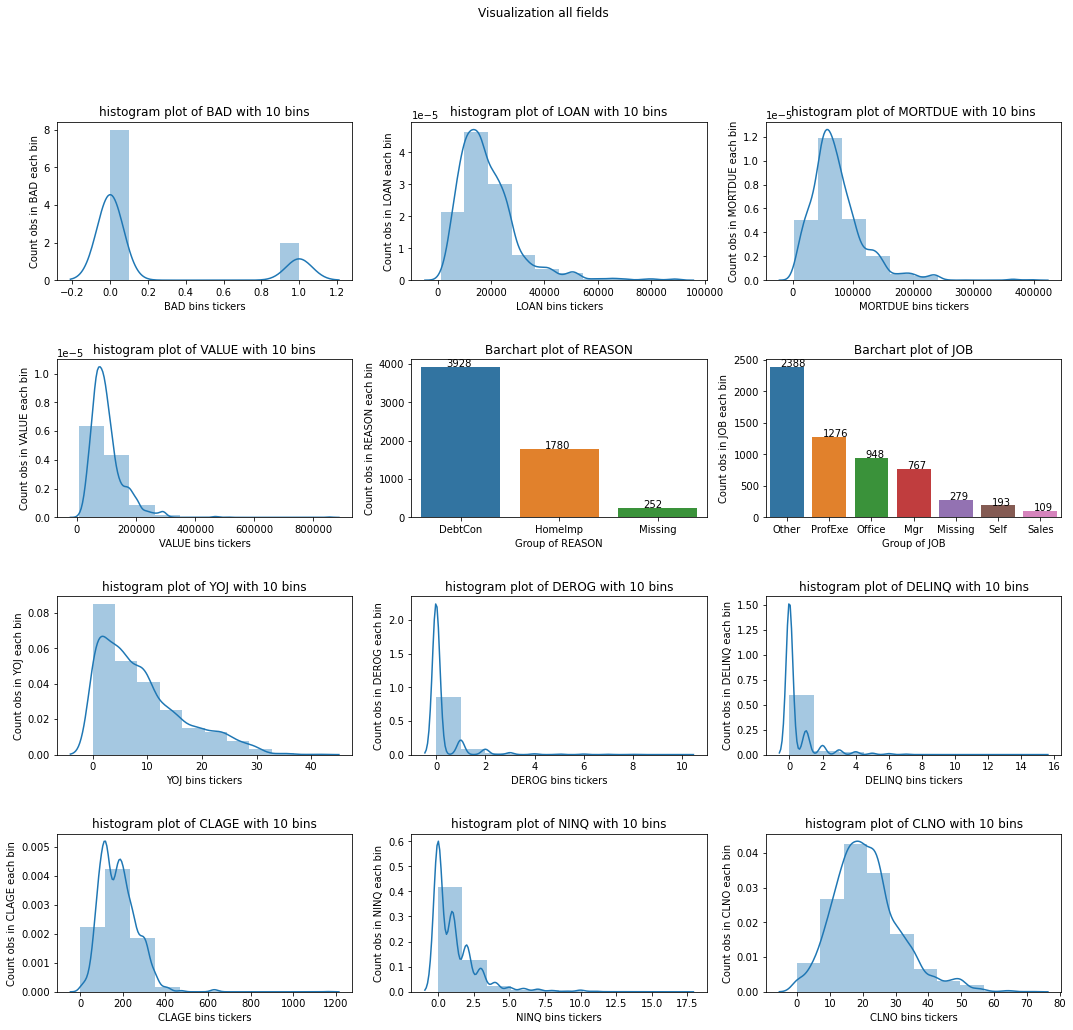
Nhận xét:

• Từ biểu đồ phân phối cho ta biết hình dạng phân phối của các biến.

• Các outliers của các biến là những điểm nào?

• Hình dạng phân phối cũng giúp ta phát hiện các dị thường trong dữ liệu. Chắc hẳn các bạn còn nhớ gian lận thi cử năm 2018 tại Sơn La và Hà Giang đã được phát hiện như thế nào?

6.2.4.2. Áp dụng phương pháp WOE

Tiếp theo ta sẽ áp dụng phương pháp WOE vào việc xếp hạng sức mạnh dự báo của biến và tạo features cho mô hình. Nhưng trước đó sẽ cần phải xử lý dữ liệu missing data bằng giá trị trung bình.

Đối với biến numeric:

columns_num = data.select_dtypes(['float', 'int']).columns
data[columns_num] = data[columns_num].apply(lambda x: x.fillna(x.mean()), axis=0)

columns_obj = data.select_dtypes(['object']).columns
data[columns_obj] = data[columns_obj].apply(lambda x: x.fillna('Missing'), axis=0)

Tính toán WOE cho từng biến

Hàm _bin_table() bên dưới sẽ có tác dụng phân chia các nhóm bins và thống kê số lượng các quan sát, số lượng good và bad ở mỗi nhóm.

import numpy as np
import matplotlib.pyplot as plt

MAX_VAL = 999999999
MIN_VAL = -MAX_VAL

def _bin_table(data, colname, n_bins = 10, qcut = None):
  X = data[[colname, 'BAD']]
  X = X.sort_values(colname)
  coltype = X[colname].dtype

  if coltype in ['float', 'int']:
    if qcut is None:
      try:
        bins, thres = pd.qcut(X[colname], q = n_bins, retbins=True)
        # Thay thế threshold đầu và cuối của thres
        thres[0] = MIN_VAL
        thres[-1] = MAX_VAL
        bins, thres = pd.cut(X[colname], bins=thres, retbins=True)
        X['bins'] = bins
      except:
        print('n_bins must be lower to bin interval is valid!')
    else:
      bins, thres = pd.cut(X[colname], bins=qcut, retbins=True)
      X['bins'] = bins
  elif coltype == 'object':
    X['bins'] = X[colname]

  df_GB = pd.pivot_table(X, 
                index = ['bins'],
                values = ['BAD'],
                columns = ['BAD'],
                aggfunc = {
                    'BAD':np.size
                })

  df_Count = pd.pivot_table(X, 
                index = ['bins'],
                values = ['BAD'],
                aggfunc = {
                    'BAD': np.size
                })
  
  if coltype in ['float', 'int']:
    df_Thres = pd.DataFrame({'Thres':thres[1:]}, index=df_GB.index)
  elif coltype == 'object':
    df_Thres = pd.DataFrame(index=df_GB.index)
    thres = None
  df_Count.columns = ['No_Obs']
  df_GB.columns = ['#BAD', '#GOOD']
  df_summary = df_Thres.join(df_Count).join(df_GB)
  return df_summary, thres

Phân chia các bins theo ngưỡng cutpoints. Phù hợp với những biến thứ bậc.

df_summary, thres = _bin_table(data, 'DELINQ', qcut=[MIN_VAL, 2, MAX_VAL])
df_summary

	Thres	No_Obs	#BAD	#GOOD
bins
(-999999999, 2]	2	5663	4674	989
(2, 999999999]	999999999	297	97	200

Phân chia các bins theo khai báo số lượng bins. Phù hợp với các biến liên tục.

df_summary, thres = _bin_table(data, 'DEBTINC', n_bins=5)
df_summary

	Thres	No_Obs	#BAD	#GOOD
bins
(-999999999.0, 29.214]	2.921447e+01	1192	1127	65
(29.214, 33.78]	3.377992e+01	2156	1316	840
(33.78, 34.688]	3.468780e+01	228	216	12
(34.688, 38.956]	3.895595e+01	1192	1102	90
(38.956, 999999999.0]	1.000000e+09	1192	1010	182

Tiếp theo hàm _WOE() sẽ tính toán các trọng số WOE ở mỗi bins và chỉ số IV cho từng biến. Trong trường hợp một bin có số lượng quan sát nhỏ hơn một ngưỡng tối thiểu ta sẽ ghép nó vào bin liền trước.

def _WOE(data, colname, n_bins = None, min_obs = 100, qcut = None):
  # Thống kê bins và lấy ra thres hold ban đầu
  df_summary, thres = _bin_table(data, colname, n_bins = n_bins, qcut = qcut)
  # Thay thế giá trị 0 của #BAD trong df_summary bằng 1 để không bị lỗi chia cho 0
  df_summary['#BAD'] = df_summary['#BAD'].replace({0:1})
  
  if qcut is not None:
    # Lọc bỏ threshold để tạo thành threshold mới mà thỏa mãn số lượng quan sát >= min_obs
    exclude_ind = np.where(df_summary['No_Obs'] <= min_obs)[0]
    if exclude_ind.shape[0] > 0:
      new_thres = np.delete(thres, exclude_ind)
      print('Auto combine {} bins into {} bins'.format(n_bins, new_thres.shape[0]-1))
      # Tính toán lại bảng summary
      df_summary, thres = _bin_table(data, colname, qcut=new_thres)
  
  new_thres = thres
  df_summary['GOOD/BAD'] = df_summary['#GOOD']/df_summary['#BAD']
  df_summary['%BAD'] = df_summary['#BAD']/df_summary['#BAD'].sum()
  df_summary['%GOOD'] = df_summary['#GOOD']/df_summary['#GOOD'].sum()
  df_summary['WOE'] = np.log(df_summary['%GOOD']/df_summary['%BAD'])
  df_summary['IV'] = (df_summary['%GOOD']-df_summary['%BAD'])*df_summary['WOE']
  df_summary['COLUMN'] = colname
  IV = df_summary['IV'].sum()
  print('Information Value of {} column: {}'.format(colname, IV))
  return df_summary, IV, new_thres

df_summary, IV, thres = _WOE(data, 'DEBTINC', n_bins = 7, min_obs= 100)
df_summary

Information Value of DEBTINC column: 1.3795573580411762

	Thres	No_Obs	#BAD	#GOOD	GOOD/BAD	%BAD	%GOOD	WOE	IV	COLUMN
bins
(-999999999.0, 27.028]	2.702826e+01	852	800	52	0.065000	0.167680	0.043734	-1.343925	0.166573	DEBTINC
(27.028, 31.875]	3.187511e+01	851	808	43	0.053218	0.169357	0.036165	-1.543919	0.205637	DEBTINC
(31.875, 33.78]	3.377992e+01	1645	835	810	0.970060	0.175016	0.681245	1.359046	0.687988	DEBTINC
(33.78, 34.043]	3.404341e+01	58	56	2	0.035714	0.011738	0.001682	-1.942761	0.019535	DEBTINC
(34.043, 37.18]	3.717985e+01	851	783	68	0.086845	0.164117	0.057191	-1.054182	0.112719	DEBTINC
(37.18, 40.133]	4.013282e+01	851	804	47	0.058458	0.168518	0.039529	-1.450008	0.187035	DEBTINC
(40.133, 999999999.0]	1.000000e+09	852	685	167	0.243796	0.143576	0.140454	-0.021982	0.000069	DEBTINC

Vẽ biểu đồ giá trị WOE của các bins.

def _plot(df_summary):
  colname = list(df_summary['COLUMN'].unique())[0]
  df_summary['WOE'].plot(linestyle='-', marker='o')
  plt.title('WOE of {} field'.format(colname))
  plt.axhline(y=0, color = 'red')
  plt.xticks(rotation=45)
  plt.ylabel('WOE')
  plt.xlabel('Bin group')

_plot(df_summary)

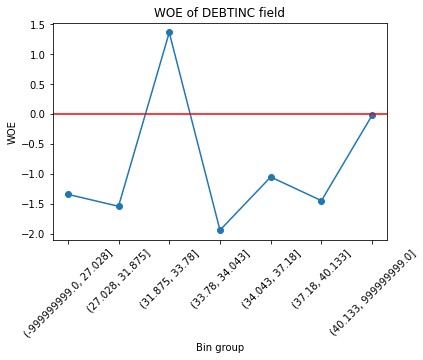
Tiếp theo ta sẽ tính toán giá trị WOE cho toàn bộ các biến.

# Đối với các biến numeric
WOE_dict=dict()
nbins = {'LOAN': 10, 'MORTDUE': 10, 'VALUE': 10, 'YOJ':10, 'CLAGE':10, 'NINQ': 2, 'CLNO':10, 'DEBTINC':7}
for (col, bins) in nbins.items():
  df_summary, IV, thres = _WOE(data, colname=col, n_bins=bins)
  WOE_dict[col] = {'table':df_summary, 'IV':IV}

Information Value of LOAN column: 0.1601563338988017
Information Value of MORTDUE column: 0.05131351983314017
Information Value of VALUE column: 0.14188912125986042
Information Value of YOJ column: 0.06714693781095009
Information Value of CLAGE column: 0.22171042878294653
Information Value of NINQ column: 0.06965935231976197
Information Value of CLNO column: 0.06043698467606807
Information Value of DEBTINC column: 1.3795573580411762

Do các biến DEROG, DELINQ có xu hướng là biến thứ bậc hơn là biến liên tục nên áp dụng cách phân chia theo quantile sẽ tạo ra những khoảng bins có độ dài bằng 0. Do đó chúng ta sẽ phân chia theo ngưỡng cutpoint.

for col in ['DEROG', 'DELINQ']:
  df_summary, IV, thres = _WOE(data, colname=col, n_bins=5, qcut=[MIN_VAL, 2, MAX_VAL])
  WOE_dict[col] = {'table':df_summary, 'IV':IV}

Information Value of DEROG column: 0.19008112833205368
Information Value of DELINQ column: 0.3366699247263777

Tiếp theo ta sẽ tính toán IV cho các biến category là REASON và JOB.

for col in ['REASON', 'JOB']:
  df_summary, IV, thres = _WOE(data, colname=col)
  WOE_dict[col] = {'table':df_summary, 'IV':IV}

Information Value of REASON column: 0.008618460238864025
Information Value of JOB column: 0.1237305657142077

6.2.4.3. Xếp hạng các biến theo sức mạnh dự báo

Dựa trên giá trị IV đã tính toán ở bước trước, ta sẽ xếp hạng các biến này như bên dưới.

columns = []
IVs = []
for col in data.columns:
  if col != 'BAD':
    columns.append(col)
    IVs.append(WOE_dict[col]['IV'])
df_WOE = pd.DataFrame({'column': columns, 'IV': IVs})

def _rank_IV(iv):
  if iv <= 0.02:
    return 'Useless'
  elif iv <= 0.1:
    return 'Weak'
  elif iv <= 0.3:
    return 'Medium'
  elif iv <= 0.5:
    return 'Strong'
  else:
    return 'Suspicious'

df_WOE['rank']=df_WOE['IV'].apply(lambda x: _rank_IV(x))
df_WOE.sort_values('IV', ascending=False)

	column	IV	rank
11	DEBTINC	1.379557	Suspicious
7	DELINQ	0.336670	Strong
8	CLAGE	0.221710	Medium
6	DEROG	0.190081	Medium
0	LOAN	0.160156	Medium
2	VALUE	0.141889	Medium
4	JOB	0.123731	Medium
9	NINQ	0.069659	Weak
5	YOJ	0.067147	Weak
10	CLNO	0.060437	Weak
1	MORTDUE	0.051314	Weak
3	REASON	0.008618	Useless

Như vậy trong các biến trên, biến REASON không có tác dụng trong việc phân loại hồ sơ nợ xấu. Các biến còn lại đều có tác dụng hỗ trợ một phần phân loại hồ sơ. Trong đó các biến có sức mạnh nhất là DELINQ, DEBTINC. Tiếp theo CLAGE, DEROG, LOAN, VALUE, JOB là các biến có sức mạnh trung bình. Các biến còn lại bao gồm NINQ, YOJ, CLNO và MORTDUE cũng có sức mạnh phân loại nhưng yếu hơn. DELINQ là biến có tương quan rất lớn đến việc phân loại nên chúng ta cần phải review lại giá trị của biến.

6.2.4.4. Hồi qui logistic

Phương trình hồi qui logistic trong credit scorecard sẽ không hồi qui trực tiếp trên các biến gốc mà thay vào đó giá trị WOE ở từng biến sẽ được sử dụng thay thế để làm đầu vào. Ta sẽ tính toán các biến WOE bằng cách map mỗi khoảng bin tương ứng với giá trị WOE của nó như sau:

for col in WOE_dict.keys():
  try:
    key = list(WOE_dict[col]['table']['WOE'].index)
    woe = list(WOE_dict[col]['table']['WOE'])
    d = dict(zip(key, woe))
    col_woe = col+'_WOE'
    data[col_woe] = data[col].map(d)
  except:
    print(col)

Gán giá trị input là các biến WOE và biến mục tiêu là data[‘BAD’].

X = data.filter(like='_WOE', axis = 1)
y = data['BAD']

Phân chia tập huấn luyện/kiểm tra có tỷ lệ kích thước mẫu là 80:20. Tỷ lệ của GOOD/BAD là cân bằng trên cả tập huấn luyện và kiểm tra.

from sklearn.model_selection import train_test_split

ids = np.arange(X.shape[0])
X_train, X_test, y_train, y_test, id_train, id_test = train_test_split(X, y, ids, test_size = 0.2, stratify = y, shuffle = True, random_state = 123)

print('X_train shape: ', X_train.shape)
print('X_test shape: ', X_test.shape)
print('y_train shape: ', y_train.shape)
print('y_test shape: ', y_test.shape)

X_train shape:  (4768, 12)
X_test shape:  (1192, 12)
y_train shape:  (4768,)
y_test shape:  (1192,)

Xây dựng phương trình hồi qui logistic các biến đầu vào WOE.

from sklearn.linear_model import LogisticRegression

logit_model = LogisticRegression(solver = 'lbfgs', max_iter=1000, fit_intercept=True, tol=0.0001, C=1, penalty='l2')
logit_model.fit(X_train, y_train)

LogisticRegression(C=1, max_iter=1000)

Dự báo và kiểm tra accuracy trên tập huấn luyện/kiểm tra

from sklearn.metrics import accuracy_score

y_pred_train = logit_model.predict(X_train)
acc_train = accuracy_score(y_pred_train, y_train)
y_pred_test = logit_model.predict(X_test)
acc_test = accuracy_score(y_pred_test, y_test)

print('accuracy on train: ', acc_train)
print('accuracy on test: ', acc_test)

accuracy on train:  0.8655620805369127
accuracy on test:  0.8557046979865772

Đường cong ROC trên tập kiểm tra

from sklearn.metrics import roc_curve, auc

y_pred_prob_test = logit_model.predict_proba(X_test)[:, 1]
fpr, tpr, thres = roc_curve(y_test, y_pred_prob_test)
roc_auc = auc(fpr, tpr)

def _plot_roc_curve(fpr, tpr, thres, auc):
    plt.figure(figsize = (10, 8))
    plt.plot(fpr, tpr, 'b-', color='darkorange', lw=2, linestyle='--', label='ROC curve (area = %0.2f)'%auc)
    plt.plot([0, 1], [0, 1], '--')
    plt.axis([0, 1, 0, 1])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.legend(loc='lower right')
    plt.title('ROC Curve')

_plot_roc_curve(fpr, tpr, thres, roc_auc)

/tmp/ipykernel_44490/1988037723.py:9: UserWarning: linestyle is redundantly defined by the 'linestyle' keyword argument and the fmt string "b-" (-> linestyle='-'). The keyword argument will take precedence.
  plt.plot(fpr, tpr, 'b-', color='darkorange', lw=2, linestyle='--', label='ROC curve (area = %0.2f)'%auc)
/tmp/ipykernel_44490/1988037723.py:9: UserWarning: color is redundantly defined by the 'color' keyword argument and the fmt string "b-" (-> color='b'). The keyword argument will take precedence.
  plt.plot(fpr, tpr, 'b-', color='darkorange', lw=2, linestyle='--', label='ROC curve (area = %0.2f)'%auc)

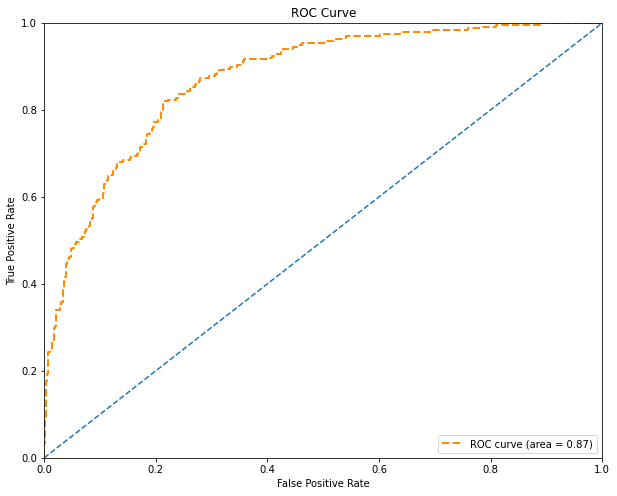
Chỉ số AUC (area under curve) đo lường phần diện tích nằm dưới đường cong ROC cho biết khả năng phân loại của các hợp đồng GOOD/BAD của mô hình hồi qui Logistic là mạnh hay yếu. AUC \(\in [0, 1]\) , giá trị của nó càng lớn thì mô hình càng tốt. Đối với mô hình hồi qui Logistic này, AUC = 0.87 là khá cao, cho thấy khả năng dự báo của mô hình tốt và có thể áp dụng mô hình vào thực tiễn.

Đường cong precision-recall trên tập kiểm tra

from sklearn.metrics import precision_recall_curve
precision, recall, thres = precision_recall_curve(y_test, y_pred_prob_test)

def _plot_prec_rec_curve(prec, rec, thres):
    plt.figure(figsize = (10, 8))
    plt.plot(thres, prec[:-1], 'b--', label = 'Precision')
    plt.plot(thres, rec[:-1], 'g-', label = 'Recall')
    plt.xlabel('Threshold')
    plt.ylabel('Probability')
    plt.title('Precsion vs Recall Curve')
    plt.legend()

_plot_prec_rec_curve(precision, recall, thres)

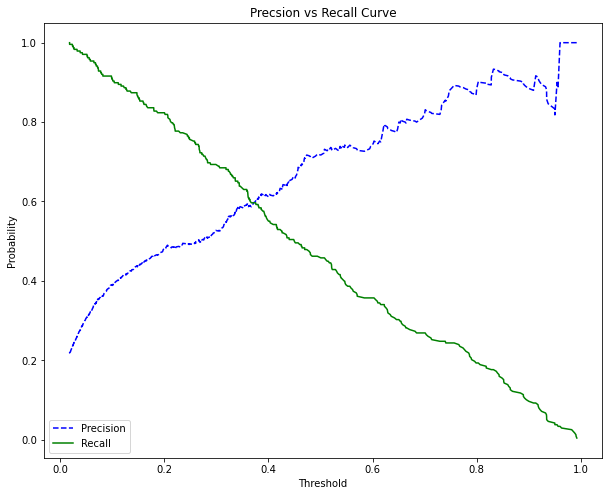
Đường cong precision-recall cho chúng ta thấy sự đánh đổi qua lại giữa độ chuẩn xác (precision) và độ phủ (recall). Dựa trên kì vọng về độ chuẩn xác hoặc độ phủ từ trước chúng ta có thể lựa chọn được ngưỡng threshold phù hợp. Chẳng hạn trước khi bước vào dự án ta kì vọng tỷ lệ dự báo đúng hồ sơ GOOD là 70% thì cần thiết lập các threshold để giá trị recall >= 70%. Trường hợp khác, ta kì vọng tỷ lệ dự báo đúng trong số các hồ sơ được dự báo là GOOD là 70% thì cần lựa chọn các threshold để giá trị precision >= 70%. Rất khó để nói ngưỡng threshold nào nên được lựa chọn là tốt nhất. Điều này phụ thuộc vào mục tiêu của mô hình là ưu tiên phân loại đúng hồ sơ GOOD hay hồ sơ BAD hơn.

Kiểm định Kolmogorov-Smirnov

Đây là kiểm định về sự khác biệt trong phân phối giữa phân phối xác suất tích luỹ giữa GOOD và BAD. Nếu mô hình có khả năng phân loại GOOD và BAD tốt thì đường cong phân phối xác suất tích lũy (cumulative distribution function - cdf) giữa GOOD và BAD phải có sự khác biệt lớn. Trái lại, nếu mô hình rất yếu và kết quả dự báo của nó chỉ ngang bằng một phép lựa chọn ngẫu nhiên. Khi đó đường phân phối xác suất tích lũy của GOOD và BAD sẽ nằm sát nhau và tiệm cận đường chéo 45 độ. Kiểm định Kolmogorov-Smirnov sẽ kiểm tra giả thuyết \(H_0\) cho rằng hai phân phối xác suất giữa GOOD và BAD không có sự khác biệt. Khi P-value < 0.05 bác bỏ giả thuyết \(H_0\).

Tính toán phân phối xác suất tích lũy của GOOD và BAD

def _KM(y_pred, n_bins):
  _, thresholds = pd.qcut(y_pred, q=n_bins, retbins=True)
  cmd_BAD = []
  cmd_GOOD = []
  BAD_id = set(np.where(y_test == 0)[0])
  GOOD_id = set(np.where(y_test == 1)[0])
  total_BAD = len(BAD_id)
  total_GOOD = len(GOOD_id)
  for thres in thresholds:
    pred_id = set(np.where(y_pred <= thres)[0])
    # Đếm % số lượng hồ sơ BAD có xác suất dự báo nhỏ hơn hoặc bằng thres
    per_BAD = len(pred_id.intersection(BAD_id))/total_BAD
    cmd_BAD.append(per_BAD)
    # Đếm % số lượng hồ sơ GOOD có xác suất dự báo nhỏ hơn hoặc bằng thres
    per_GOOD = len(pred_id.intersection(GOOD_id))/total_GOOD
    cmd_GOOD.append(per_GOOD)
  cmd_BAD = np.array(cmd_BAD)
  cmd_GOOD = np.array(cmd_GOOD)
  return cmd_BAD, cmd_GOOD, thresholds

cmd_BAD, cmd_GOOD, thresholds = _KM(y_pred_prob_test, n_bins=20)

Biểu đồ phân phối xác suất tích lũy của GOOD và BAD

def _plot_KM(cmd_BAD, cmd_GOOD, thresholds):
  plt.figure(figsize = (10, 8))
  plt.plot(thresholds, cmd_BAD, 'y-', label = 'BAD')
  plt.plot(thresholds, cmd_GOOD, 'g-', label = 'GOOD')
  plt.plot(thresholds, cmd_BAD-cmd_GOOD, 'b--', label = 'DIFF')
  plt.xlabel('% observation')
  plt.ylabel('% total GOOD/BAD')
  plt.title('Kolmogorov-Smirnov Curve')
  plt.legend()

_plot_KM(cmd_BAD, cmd_GOOD, thresholds)

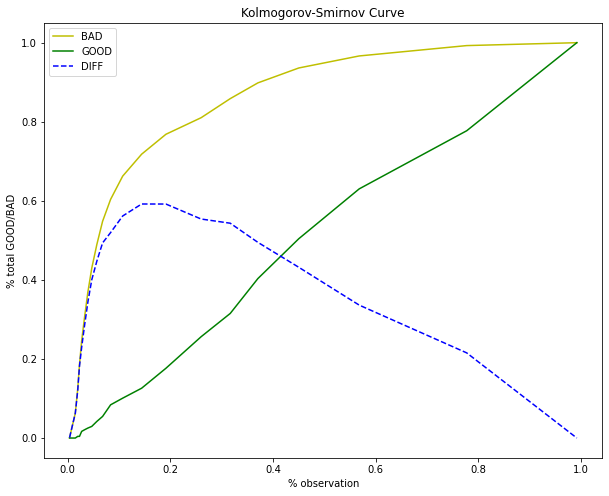
Kiểm định Kolmogorov-Smirnov:

from scipy import stats

stats.ks_2samp(cmd_BAD, cmd_GOOD)

KstestResult(statistic=0.5238095238095238, pvalue=0.005467427576534314)

p-value < 0.05 cho thấy phân phối tích lũy giữa tỷ lệ BAD và GOOD là khác biệt nhau. Do đó mô hình có ý nghĩa trong phân loại hồ sơ.

6.2.4.5. Tính điểm credit score cho mỗi đặc trưng

Bước cuối cùng là tính ra điểm tín nhiệm (credit scorecard) của mỗi khách hàng bằng cách tính điểm số cho mỗi đặc trưng (đặc trưng) ở đây là một khoảng bin của biến liên tục hoặc một nhãn của biến hạng mục). Điểm sẽ được scale theo công thức sau:

\[\text{Score} = (\beta.\text{WOE}+\frac{\alpha}{n}).\text{Factor}+\frac{\text{Offset}}{n} \tag{1}\]

Trong đó:

• \(\beta\): Hệ số của biến đặc trưng đầu vào trong phương trình hồi qui Logistic.

• \(\alpha\): Hệ số chặn của phương trình hồi qui Logistic.

• \(\text{WOE}\): Giá trị của biến đặc trưng đầu vào đã được gán bằng giá trị với WOE.

• \(n\): Số lượng các biến của mô hình.

\(\text{Factor}, \text{Offset}\) Là các tham số được thiết lập để tính Score. Chúng được tính từ \(\text{pdo}\) và \(\text{odd}\) theo công thức:

• \(\text{Factor} = \frac{\text{pdo}}{\ln(2)}\)

• \(\text{Offset} = \text{Base_Score}-(\text{Factor}.\ln(\text{odd}))\)

Diễn giải ý nghĩa của Offset và Factor

Như chúng ta đã biết, \(\text{odd}\) chính là tỷ lệ giữa xác suất GOOD/BAD.

Gỉa sử xác suất để hợp đồng là GOOD bằng \(p\) thì tỷ lệ:

\[\text{odd} = \frac{p}{1-p}\]

\(p\) được tính theo hàm Sigmoid. Nên giá trị:

\[\ln(\text{odd}) = \ln{(\frac{p}{1-p})} = \ln{(e^{\beta \mathbf{x}})} = \beta \mathbf{x}\]

Nếu coi \(\frac{\text{Offset}}{n}=C\) là một hằng số. Như vậy phương trình (1) ta có thể viết thành:

\[\text{Score} = (\ln(\text{odd})*\text{Factor}) + C\]

Lấy đạo hàm theo \(\ln(\text{odd})\):

\[\text{Factor} = \frac{d ~\text{Score}}{d ~\ln(\text{odd})}\]

Ý nghĩa của Factor:

Gỉa sử với mức điểm cơ sở (\(\text{Base_score}\)) là \(600\) thì tỷ lệ odd ratio là \(1:30\). Điểm càng cao thì hồ sơ càng tốt, do đó khi mức điểm giảm xuống còn \(580\) thì tỷ lệ hồ sơ xấu (nhãn GOOD) tăng lên và khiến cho tỷ lệ odd ratio tăng gấp đôi thành \(1:15\). Chúng ta có thể hiểu \(\text{pdo}\) (point double odd ratio) chính là điểm thay đổi để gấp đôi tỷ lệ odd, giả sử chúng có giá trị bằng -20. Khi đó:

\[\text{Factor} = \frac{d ~\text{Score}}{d ~\ln(\text{odd})} = \frac{\text{pdo}}{\ln(2)} \tag{2}\]

Như vậy \(\text{Factor}\) chính là tác động biên khi gia tăng odd ratio gấp đôi lên điểm số ứng với mỗi đặc trưng.

Ý nghĩa của Offset:

\(\text{Offset}\) có thể được xem như phần bù của điểm số để đạt được mức điểm \(\text{Base_score}\).

Để hình dung rõ hơn quá trình tính điểm score chúng ta lấy ví dụ:

Một mô hình credit scorecard có các tham số thiết lập gồm tỷ lệ \(\text{odd} = 1:50\) tại \(\text{Base_Score} =600\) điểm và \(\text{pdo}=20\), hai tham số \(\text{Factor}, \text{Offset}\) được tính như sau:

• \(\text{Factor}=\frac{20}{\ln(2)}=28.85\)

• \(\text{Offset}=600-28.85\times \ln(1/50)=712.86\)

Phương trình hồi qui có hệ số đối với 1 biến bất kì là \(\beta = 0.5\), hệ số tự do \(\alpha=1\), giá trị \(\text{WOE}=0.15\) và số lượng các biến \(n=12\). Khi đó áp dụng phương trình (1) tính điểm tín nhiệm \(\text{Score}\) được đóng góp bởi biến đó sẽ là:

\[\text{Score} = (0.5\times0.15+\frac{1}{12}).\text{28.85}+\frac{\text{712.85}}{12} = 63.97\]

Ta có thể tạo ra hàm số tính điểm cho mỗi đặc trưng như sau:

import numpy as np

def _CreditScore(beta, alpha, woe, n = 12, odds = 1/4, pdo = -50, thres_score = 600):
  factor = pdo/np.log(2)
  offset = thres_score - factor*np.log(odds)
  score = (beta*woe+alpha/n)*factor+offset/n
  return score

_CreditScore(beta = 0.5, alpha = -1, woe = 0.15, n = 12)

42.2677896003704

Gán các giá trị \(\beta\) và \(\alpha\) vào dictionary.

betas_dict = dict(zip(list(X_train.columns), logit_model.coef_[0]))
alpha = logit_model.intercept_[0]
betas_dict

{'LOAN_WOE': 0.4710324107004053,
 'MORTDUE_WOE': 0.5825609027920233,
 'VALUE_WOE': 0.7543949126408708,
 'YOJ_WOE': 0.883788791405289,
 'CLAGE_WOE': 0.8622728924386148,
 'NINQ_WOE': 0.5431039926781012,
 'CLNO_WOE': 0.8543750687914761,
 'DEBTINC_WOE': 0.9440898350669943,
 'DEROG_WOE': 0.9016268860831372,
 'DELINQ_WOE': 1.054952732547523,
 'REASON_WOE': 0.6474770785463526,
 'JOB_WOE': 0.8871024491457584}

Tính WOE cho từng đặc trưng.

cols = []
features = []
woes = []
betas = []
scores = []

for col in columns:
  for feature, woe in WOE_dict[col]['table']['WOE'].to_frame().iterrows():
      cols.append(col)
      # Add feature
      feature = str(feature)
      features.append(feature)    
      # Add woe
      woe = woe.values[0]
      woes.append(woe)
      # Add beta
      col_woe = col+'_WOE'
      beta = betas_dict[col_woe]
      betas.append(beta)
      # Add score
      score = _CreditScore(beta = beta, alpha = alpha, woe = woe, n = 12)
      scores.append(score)

df_WOE = pd.DataFrame({'Columns': cols, 'Features': features, 'WOE': woes, 'Betas':betas, 'Scores':scores})
df_WOE.head()

	Columns	Features	WOE	Betas	Scores
0	LOAN	(-999999999.0, 7600.0]	0.898910	0.471032	19.446581
1	LOAN	(7600.0, 10000.0]	0.154566	0.471032	44.737736
2	LOAN	(10000.0, 12100.0]	-0.112535	0.471032	53.813262
3	LOAN	(12100.0, 14400.0]	-0.158318	0.471032	55.368853
4	LOAN	(14400.0, 16300.0]	0.162082	0.471032	44.482362

Như vậy ta đã hoàn thiện bảng tính điểm số cho mỗi features. Từ điểm số này ta có thể suy ra điểm tín nhiệm của mỗi một hồ sơ bằng cách tính tổng điểm số của toàn bộ các features của hồ sơ đó. Bên dưới ta sẽ thực hành tính điểm tín nhiệm cho một hồ sơ ngẫu nhiên:

# Giả sử một hồ sơ ngẫu nhiên có các thông số như sau
test_obs = data[columns].iloc[0:1, :]
test_obs

	LOAN	MORTDUE	VALUE	REASON	JOB	YOJ	DEROG	DELINQ	CLAGE	NINQ	CLNO	DEBTINC
0	1100	25860.0	39025.0	HomeImp	Other	10.5	0.0	0.0	94.366667	1.0	9.0	33.779915

Viết hàm tính toán điểm số cho mỗi trường của một bộ hồ sơ:

def _search_score(obs, col):
  feature = [str(inter) for inter in list(WOE_dict[col]['table'].index) if obs[col].values[0] in inter][0]
  score = df_WOE[(df_WOE['Columns'] == col) & (df_WOE['Features'] == feature)]['Scores'].values[0]
  return score

# Tính điểm cho trường 'LOAN' của bộ hồ sơ test
score = _search_score(test_obs, 'LOAN')
score

19.446580780492287

Điểm chi tiết của từng trường trong bộ hồ sơ và điểm của toàn bộ bộ hồ sơ sẽ là:

def _total_score(obs, columns = columns):
  scores = dict()
  for col in columns:
    scores[col] = _search_score(obs, col)
  total_score = sum(scores.values())
  return scores, total_score

scores, total_score = _total_score(test_obs)

Ta có thể tính toán điểm tín nhiệm cho toàn bộ các hồ sơ trên tập huấn luyện như sau:

total_scores = []
data_test = data.iloc[id_test].copy()
for i in np.arange(data_test[columns].shape[0]):
  obs = data_test[columns].iloc[i:(i+1), :]
  _, score = _total_score(obs)
  total_scores.append(score)

data_test['Score'] = total_scores

Biểu đồ phân phối của điểm số theo GOOD và BAD

plt.figure(figsize=(16, 4))
plt.subplot(121)
sns.distplot(data_test['Score'])
plt.title('Distribution Score of Total data')
plt.subplot(122)
sns.distplot(data_test[data_test['BAD']==1]['Score'], label='Default')
sns.distplot(data_test[data_test['BAD']==0]['Score'], label='Non-Default', 
             kde_kws={"color": "r"}, 
             hist_kws={"color": "g", "alpha":0.5})
plt.legend(loc = 'lower right')
plt.title('Distribution Score in Default vs Non-Default')

Text(0.5, 1.0, 'Distribution Score in Default vs Non-Default')

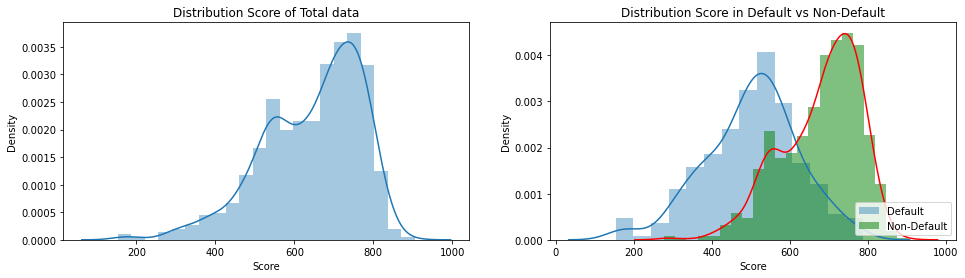
Như vậy ta có thể nhận thấy phân phối điểm số của hồ sơ Default và Non-Default là khác biệt nhau. Điểm số tín nhiệm đánh giá mức độ tin cậy của khách hàng về khả năng trả nợ cho ngân hàng. Một khách hàng có điểm số tín nhiệm cao sẽ gia tăng mức độ tin tưởng của Ngân hàng dành cho họ. Ngoài ra Ngân hàng cũng có thể dựa trên điểm tín nhiệm để phân loại khách hàng thành những nhóm tiềm năng khác nhau giống như chỉ số FICO score đã phân loại:

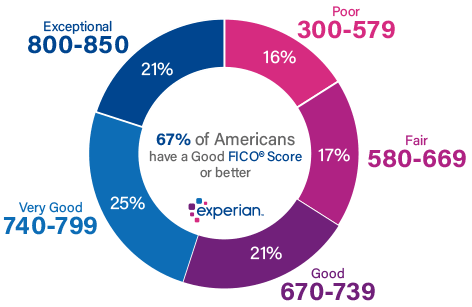
Hình 1: Tỷ lệ phân chia các nhóm khách hàng theo ngưỡng điểm tín nhiệm.

Bên dưới là bảng thống kê đối với danh mục khách hàng vay vốn theo điểm scorecard.

Bảng 2: Bảng ảnh hưởng của các nhóm khách hàng theo điểm tín nhiệm.

Để giảm thiểu rủi ro thì Ngân hàng có thể đưa ra các điều kiện ràng buộc khi cho vay. Chẳng hạn như đối với khách hàng rơi vào nhóm Very Poor, Ngân hàng có thể đề nghị khách trả phí vay và tiền đặt cọc hoặc thậm chí là không cho vay với nhóm khách hàng này.

6.3. Kết luận

Như vậy tôi đã giới thiệu tới các bạn các bước để xây dựng một mô hình credit scorecard từ các bước như thu thập dữ liệu, tiền xử lý dữ liệu bằng phương pháp WOE, hồi qui mô hình, hậu kiểm mô hình, dự báo xác suất, tính toán điểm tín nhiệm cho một hồ sơ. Về cơ bản phương pháp scorecard là khá đơn giản. Tuy nhiên quá trình xây dựng mô hình đòi hỏi phải đáp ứng được rất nhiều tiêu chí như khả năng giải thích, độ chính xác, chi phí xây dựng, khả năng áp dụng vào thực tiễn. Điều này đòi hỏi chúng ta phải bỏ ra nhiều công sức hơn để huấn luyện và cải tiến mô hình scorecard.

Bên cạnh đó, ngoài áp dụng trong lĩnh vực quản trị rủi ro tín dụng, mô hình scorecard còn có thể mở rộng và áp dụng sang rất nhiều các lĩnh vực khác như thẩm định khách hàng trên các nền tảng cho vay online, xếp hạng khách hàng trong marketing, xếp hạng doanh nghiệp, xếp hạng quốc gia, tổ chức tài chính,…

6.4. Bài tập

Sử dụng bộ dữ liệu về churn customer. Hãy thực hiện các công việc sau.

1. Khảo sát dữ liệu đầu vào.

2. Phân chia hai tập huấn luyện và kiểm tra theo tỷ lệ 80:20.

3. Tính toán chỉ số WOE trên từng biến và xếp hạng sức mạnh phân loại của từng biến.

4. Xây dựng mô hình scorecard trên tập huấn luyện.

5. Chấm điểm khách hàng rời bỏ trên tập kiểm tra.

6. Đánh giá sự khác biệt về phân phối giữa hai xác suất luỹ kế giữa GOOD và BAD.

6.5. Tài liệu tham khảo

1. FICO score

2. WOE - Weight of Evidence

3. Scorecard model - Nguyen Chi Dung VietNam

4. Introduction to credit scoring and scorecard approach - Jenny Nguyen

5. Introduction to credit scoring and scorecard approach- Nguyen Chi Dung VietNam

6. Attribute relevance analysis in python IV and WOE - R language

7. Scorecard package in R language

8. Scorecard package in python

9. Creditworthiness - investopedia

10. Credit Risk Scorecards Implementing Intelligent - Naeem Siddiqui

11. Credit Scoring Application at Banks: Mapping to Basel II - Do Hoai Linh, Luong Thi Thu Hang, Nguyen Xuan Thang - NEU University VietNam

12. Credit Risk Factor Modeling and the Basel II IRB Approach

previous

6. Ứng dụng mô hình scorecard

next

7. Giới thiệu về SVM