Bài 4 - Attention is all you need

18 Jun 2019 - phamdinhkhanh

1. Quá trình encoder và decoder

Máy tính không thể học được từ các dữ liệu thô như bức ảnh, file text, file âm thanh, đoạn video. Do đó nó cần đến quá trình mã hóa thông tin sang dạng số và từ dạng số giải mã kết quả đầu ra. Đó chính là 2 quá trình encoder và decoder:

Encoder: Là phrase chuyển input thành những features learning có khả năng học tập các task. Đối với model Neural Network, Encoder là các hidden layer. Đối với model CNN, Encoder là chuỗi các layers Convolutional + Maxpooling. Model RNN quá trình Encoder chính là các layers Embedding và Recurrent Neral Network.
Decoder: Đầu ra của encoder chính là đầu vào của các Decoder. Phrase này nhằm mục đích tìm ra phân phối xác xuất từ các features learning ở Encoder từ đó xác định đâu là nhãn của đầu ra. Kết quả có thể là một nhãn đối với các model phân loại hoặc một chuỗi các nhãn theo tứ tự thời gian đối với model seq2seq.

RNN là model thuộc lớp seq2seq. Về định nghĩa của model chúng ta có thể xem lại bài tổng hợp sau: RNN - Khanh Blog Các kĩ thuật RNN đã trải qua rất nhiều những tiến bộ với nhiều kiến trúc được giới thiệu như LSTM, GRU để khắc phục hạn chế về khả năng học phụ thuộc dài hạn. Tuy nhiên trong nhiều bài toán về dịch thuật, việc cải thiện cũng không đáng kể. Chính vì thế kĩ thuật attention được áp dụng để mang lại hiệu quả cao hơn.

Mô hình seq2seq là mô hình chuỗi nên có thứ tự về thời gian. Trong một tác vụ dịch máy, các từ ở input sẽ có mối liên hệ lớn hơn đối với từ ở output cùng vị trí. Do đó attention hiểu một cách đơn giản sẽ giúp thuật toán điều chỉnh sự tập trung lớn hơn ở các cặp từ (input, output) nếu chúng có vị trí tương đương hoặc gần tương đương.

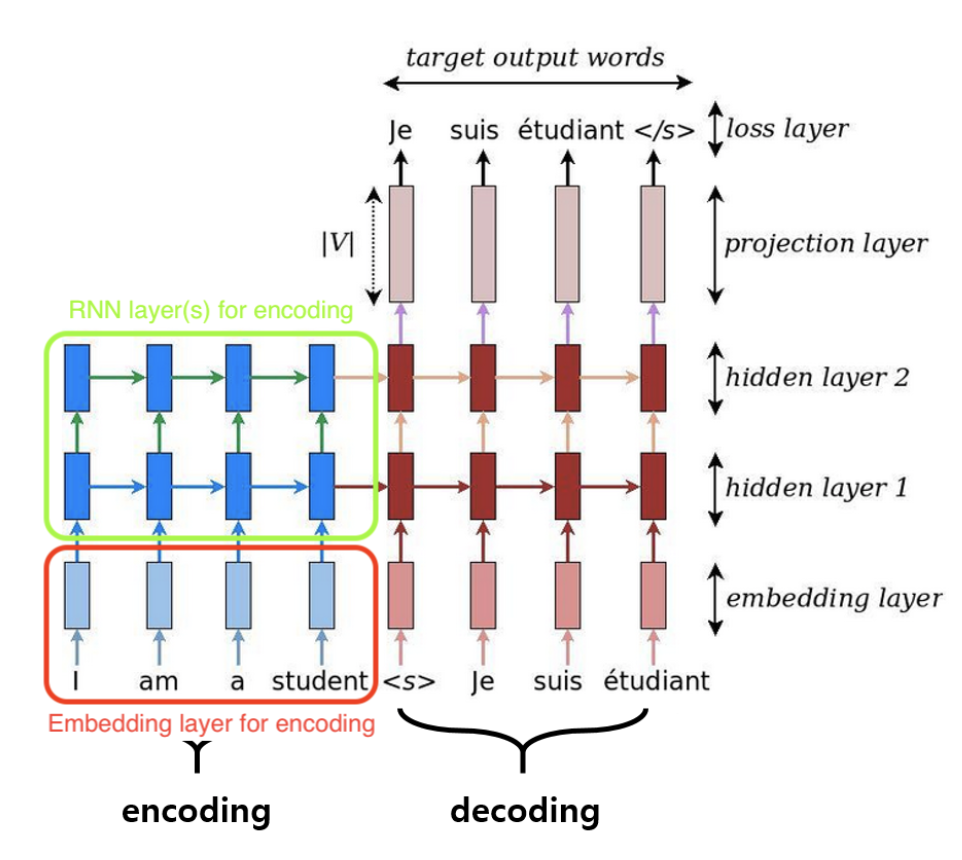
Hình 1:Mô hình seq2seq khi chưa có attention layer

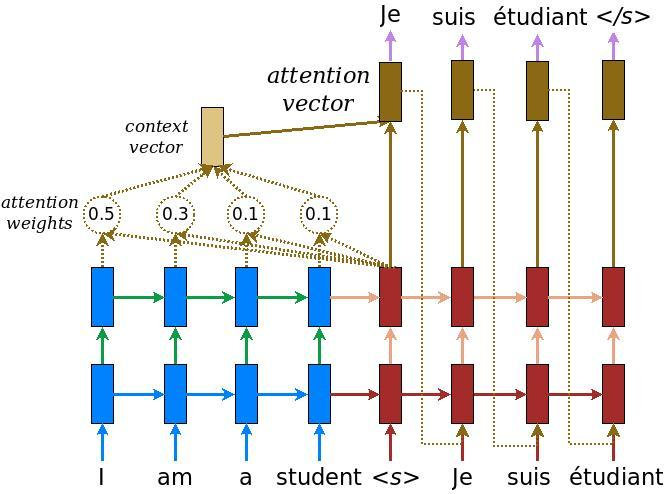
Hình 2:Mô hình seq2seq khi đã có attention layer

Như trong hình 2, Từ ‘I’ trong tiếng anh tương ứng với ‘Je’ trong tiếng Pháp. Do đó attention layer điều chỉnh một trọng số $\alpha$ lớn hơn ở context vector so với các từ khác.

Màu xanh đại diện cho encoder và màu đỏ đại diện cho decoder. Các thẻ màu xanh chính là các hidden state $h_t$ được trả ra ở mỗi unit (trong keras, khi khởi tạo RNN chúng ta sử dụng tham số return_sequences = True để trả ra các hidden state, trái lại chỉ trả ra hidden state ở unit cuối cùng). Chúng ta thấy context vector chính là tổ hợp tuyến tính của các output theo trọng số attention. Ở vị trí thứ nhất của phase decoder thì context véc tơ sẽ phân bố trọng số attention cao hơn so với các vị trí còn lại. Điều đó thể hiện rằng véc tơ context tại mỗi time step sẽ ưu tiên bằng cách đánh trọng số cao hơn cho các từ ở cùng vị trí time step. Ưu điểm khi sử dụng attention đó là mô hình lấy được toàn bộ bối cảnh của câu thay vì chỉ một từ input so với model ở hình 1 khi không có attention layer. Cơ chế xây dựng attention layer là một qui trình khá đơn giản. Chúng ta sẽ trải qua các bước:

1. Đầu tiên tại time step thứ $t$ ta tính ra list các điểm số, mỗi điểm tương ứng với một cặp vị trí input $t$ và các vị trí còn lại theo công thức bên dưới:

\[score(h_t, \bar{h_s})\]

Ở đây $h_t$ cố định tại time step $t$ và là hidden state của từ mục tiêu thứ $t$ ở phase decoder, $\bar{h_s}$ là hidden state của từ thứ $s$ trong phase encoder. Công thức để tính score có thể là dot product hoặc cosine similarity tùy vào lựa chọn.

2. Các scores sau bước 1 chưa được chuẩn hóa. Để tạo thành một phân phối xác xuất chúng ta đi qua hàm softmax khi đó ta sẽ thu được các trọng số attention weight.

\[\alpha_{ts} = \frac{\text{exp}(score(h_t, \bar{h_s}))}{\sum_{s'=1}^{S}\text{exp}(score(h_t, \bar{h_{s'}}))}\]

$\alpha_{ts}$ là phân phối attention (attention weight) của các từ trong input tới các từ ở vị trí $t$ trong output hoặc target.

3. Kết hợp vector phân phối xác xuất $\alpha_{ts}$ với các vector hidden state để thu được context vector.

\[c_t = \sum_{s'=1}^{S} \alpha_{ts}\bar{h_{s'}}\]

4. Tính attention vector để decode ra từ tương ứng ở ngôn ngữ đích. Attention vector sẽ là kết hợp của context vector và các hidden state ở decoder. Theo cách này attention vector sẽ không chỉ được học từ chỉ hidden state ở unit cuối cùng như hình 1 mà còn được học từ toàn bộ các từ ở vị trí khác thông qua context vector. Công thức tính output cho hidden state cũng tương tự như tính đầu ra cho input gate layer trong mạng RNN:

\[a_t = f(c_t, h_t) = tanh(\mathbf{W_c}[c_t, h_t])\]

Kí hiệu $[c_t, h_t]$ là phép concatenate 2 vector $c_t, h_t$ theo chiều dài. Giả sử $c_t \in \mathbb{R}^{c}$, $h_t \in \mathbb{R}^{h}$ thì vector $[c_t, h_t] \in \mathbb{R}^{c+h}$. $\mathbf{W_c} \in \mathbb{R}^{a\times(c+h)}$ trong đó $a$ là độ dài của attention vector. Ma trận mà chúng ta cần huấn luyện chính là $\mathbf{W_c}$

2. Transformer và Seq2Seq model

Ý tưởng chính của bài viết này được lấy từ bài báo attention is all you need giới thiệu về các kiểu attention model được sử dụng trong các tác vụ học máy. Trong bài báo cũng đưa ra một kiến trúc mới về Transformer hoàn toàn khác so với các kiến trúc RNN trước đây, mặc dù cả 2 đều thuộc lớp model seq2seq nhằm chuyển 1 câu văn input ở ngôn ngữ A sang 1 câu văn output ở ngôn ngữ B. Quá trình biến đổi (transforming) được dựa trên 2 phần encoder và decoder.

Chúng ta biết rằng RNN là lớp model tốt trong dịch máy vì ghi nhận được sự phụ thuộc thời gian của các từ trong câu. Tuy nhiên các nghiên cứu mới đã chỉ ra rằng với chỉ với cơ chế attention mà không cần đến RNN đã có thể cải thiện được kết quả của các tác vụ dịch máy và nhiều tác vụ khác. Một trong những cải thiện đó là model BERT mà bạn đọc có thể tham khảo ở link sau: Pre-training of Deep Bidirectional Transformers for Language Understanding

Vậy cụ thể Transformer là gì? Kiến trúc của Transformer ra sao chúng ta cùng tìm hiểu qua sơ đồ bên dưới:

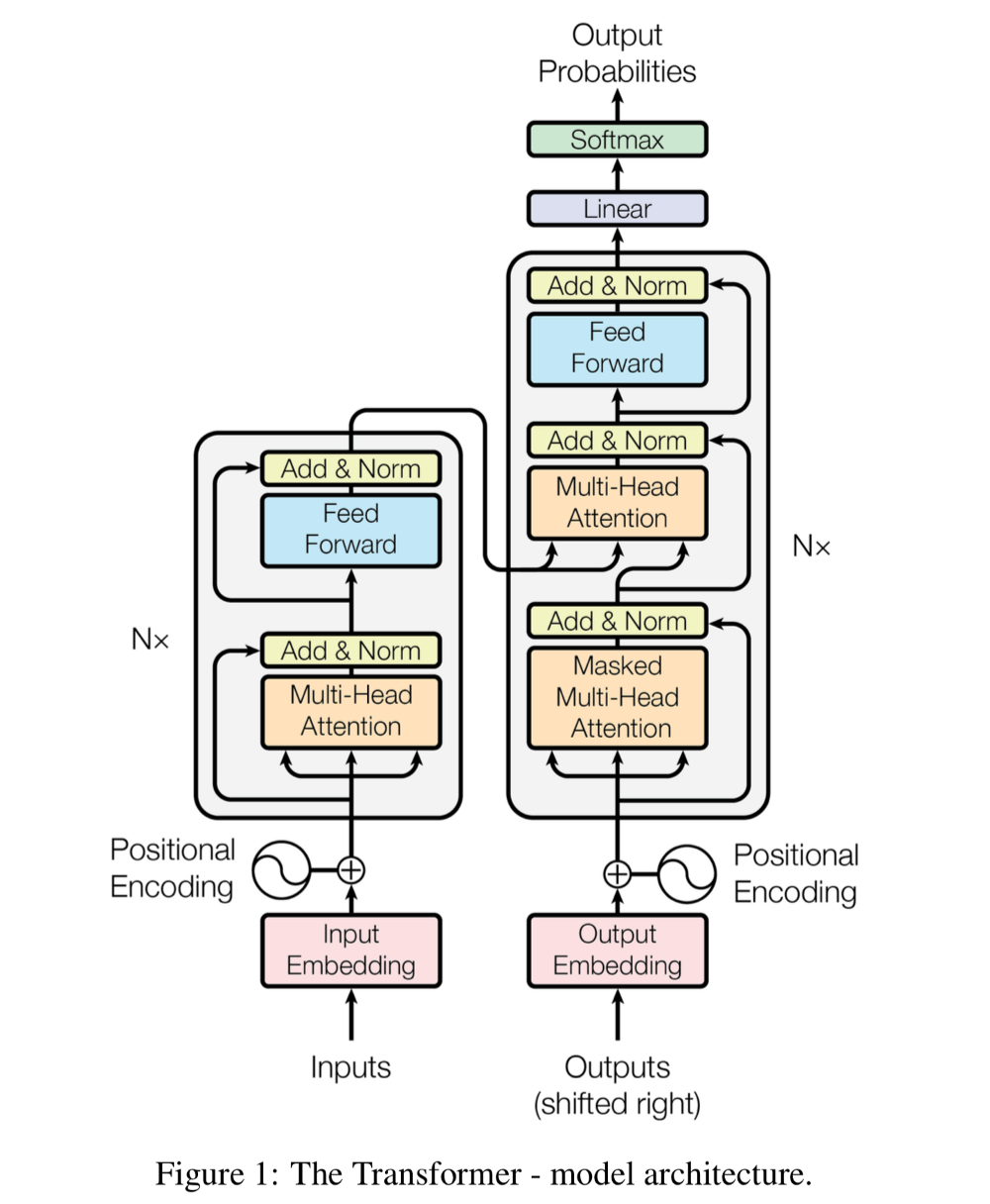
Hình 3: Kiến trúc transformer

Kiến trúc này gồm 2 phần encoder bên trái và decoder bên phải.

Encoder: là tổng hợp xếp chồng lên nhau của 6 layers xác định. Mỗi layer bao gồm 2 layer con (sub-layer) trong nó. Sub-layer đầu tiên là multi-head self-attention mà lát nữa chúng ta sẽ tìm hiểu. Layer thứ 2 đơn thuần chỉ là các fully-connected feed-forward layer. Chắc mình sẽ không giải thích thêm về fully-connected feed-forward layer nữa vì chúng là khái niệm quá cơ bản trong machine learning. Các bạn có thể tìm hiều thêm ở bài viết chi tiết này Multi-layer Perceptron của machinelearningcoban. Một lưu ý là chúng ta sẽ sử dụng một kết nối residual ở mỗi sub-layer ngay sau layer normalization. Kiến trúc này có ý tưởng tương tự như mạng resnet trong CNN. Đầu ra của mỗi sub-layer là $LayerNorm(x+Sublayer(x))$ có số chiều là 512 theo như bài viết.

Decoder: Decoder cũng là tổng hợp xếp chồng của 6 layers. Kiến trúc tương tự như các sub-layer ở Encoder ngoại trừ thêm 1 sub-layer thể hiện phân phối attention ở vị trí đầu tiên. Layer này không gì khác so với multi-head self-attention layer ngoại trừ được điều chỉnh để không đưa các từ trong tương lai vào attention. Tại bước thứ $i$ của decoder chúng ta chỉ biết được các từ ở vị trí nhỏ hơn $i$ nên việc điều chỉnh đảm bảo attention chỉ áp dụng cho những từ nhỏ hơn vị trí thứ i. Cơ chế residual cũng được áp dụng tương tự như trong Encoder.

Lưu ý là chúng ta luôn có một bước cộng thêm Positional Encoding vào các input của encoder và decoder nhằm đưa thêm yếu tố thời gian vào mô hình làm tăng độ chuẩn xác. Đây chỉ đơn thuần là phép cộng vector mã hóa vị trí của từ trong câu với vector biểu diễn từ. Chúng ta có thể mã hóa dưới dạng [0, 1] vector vị trí hoặc sử dụng hàm $sin, cos$ như trong bài báo.

3. Cơ chế Attention

3.1. Scale dot product attention

Đây chính là một cơ chế self-attention khi mỗi từ có thể điều chỉnh trọng số của nó cho các từ khác trong câu sao cho từ ở vị trí càng gần nó nhất thì trọng số càng lớn và càng xa thì càng nhỏ dần. Sau bước nhúng từ (đi qua embeding layer) ta có đầu vào của encoder và decoder là ma trận $\mathbf{X}$ kích thước $m\times n$, $m, n$ lần lượt là là độ dài câu và số chiều của một vector nhúng từ.

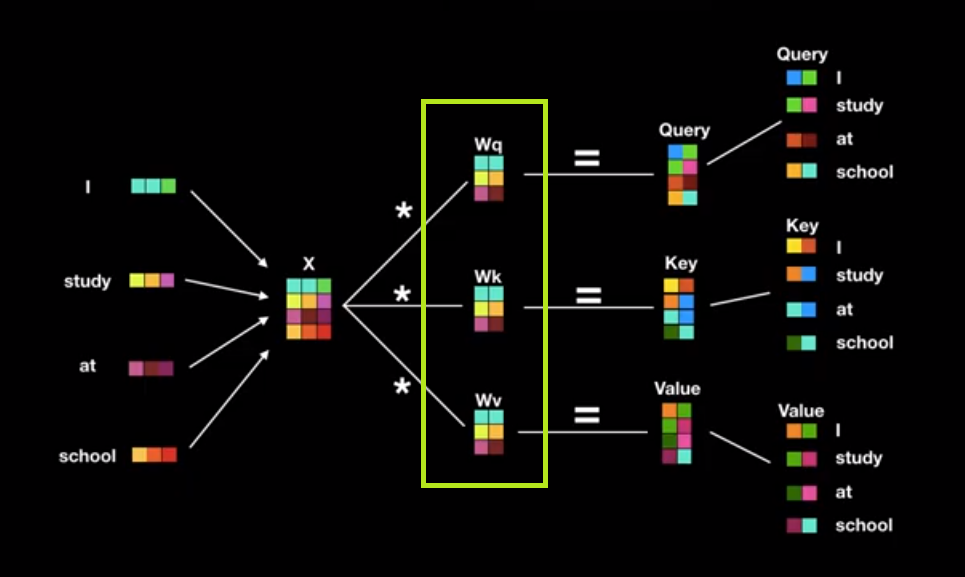
Hình 4: Self Attention. Trong khung màu vàng là 3 ma trận $\mathbf{W_q, W_k, W_v}$ chính là những hệ số mà model cần huấn luyện. Sau khi nhân các ma trận này với ma trận đầu vào $\mathbf{X}$ ta thu được ma trận $\mathbf{Q, K, V}$ (tương ứng với trong hình là ma trận Query, Key và Value). Ma trận Query và Key có tác dụng tính toán ra phân phối score cho các cặp từ (giải thích ở hình 6). Ma trận Value sẽ dựa trên phân phối score để tính ra véc tơ phân phối xác suất output.

Như vậy mỗi một từ sẽ được gán bởi 3 vector query, key và value là các dòng của $\mathbf{Q, K, V}$.

Hình 5: Các từ input tương ứng với vector key, query và value.

Để tính ra score cho mỗi cặp từ $(w_i, w_j)$, chúng ta sẽ tính toán dot-product giữa query với key, phép tính này nhằm tìm ra mối liên hệ trọng số của các cặp từ. Tuy nhiên điểm số sau cùng là điểm số chưa được chuẩn hóa. Do đó chúng ta chuẩn hóa bằng một hàm softmax để đưa về một phân phối xác xuất mà độ lớn sẽ đại diện cho mức độ attention của từ query tới từ key. Trọng số càng lớn càng chứng tỏ từ $w_i$ trả về một sự chú ý lớn hơn đối với từ $w_j$. Sau đó chúng ta nhân hàm softmax với các vector giá trị của từ hay còn gọi là value vector để tìm ra vector đại diện (attention vetor) sau khi đã học trên toàn bộ câu input.

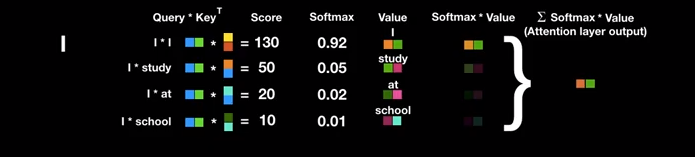
Hình 6: Quá trình tính toán trọng số attentiion và attention vector cho từ I trong câu I study at school.

Hoàn toàn tương tự khi di chuyển sang các từ khác trong câu ta cũng thu được kết quả tính toán như minh họa.

Hình 7: Kết quả tính attention vector cho toàn bộ các từ trong câu.

Từ các triển khai trên các vector dòng các bạn đã hình dung ra biến đổi cho ma trận rồi chứ?

Đầu vào để tính attention sẽ bao gồm ma trận $\mathbf{Q}$ (mỗi dòng của nó là một vector query đại diện cho các từ input), ma trận $\mathbf{K}$ (tương tự như ma trận $\mathbf{Q}$, mỗi dòng là vector key đại diện cho các từ input). Hai ma trận $\mathbf{Q, K}$ được sử dụng để tính attention mà các từ trong câu trả về cho 1 từ cụ thể trong câu. attention vector sẽ được tính dựa trên trung bình có trọng số của các vector value trong ma tận $\mathbf{V}$ với trọng số attention (được tính từ $\mathbf{Q, K}$).

Trong thực hành chúng ta tính toán hàm attention trên toàn bộ tập các câu truy vấn một cách đồng thời được đóng gói thông qua ma trận $\mathbf{Q}$. keys và values cũng được đóng gói cùng nhau thông qua matrix $\mathbf{K}$ và $\mathbf{V}$. Phương trình Attention như sau:

\[Attention(\mathbf{Q, K, V}) = softmax(\frac{\mathbf{QK^T})}{\sqrt{d_k}}\mathbf{V} \tag{1}\]

Việc chia cho $d_k$ là số dimension của vector key nhằm mục đích tránh tràn luồng nếu số mũ là quá lớn.

3.2. Multi-head Attention

Như vậy sau quá trình Scale dot production chúng ta sẽ thu được 1 ma trận attention. Các tham số mà model cần tinh chỉnh chính là các ma trận $\mathbf{W_q, W_k, W_v}$. Mỗi quá trình như vậy được gọi là 1 head của attention. Khi lặp lại quá trình này nhiều lần (trong bài báo là 3 heads) ta sẽ thu được quá trình Multi-head Attention như biến đổi bên dưới:

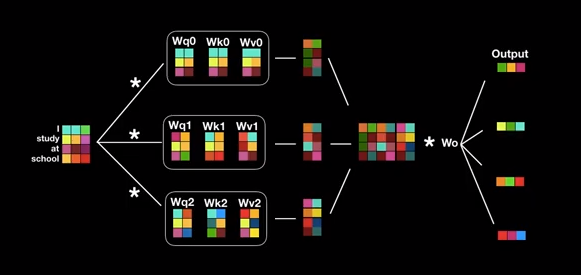
Hình 8: Sơ đồ cấu trúc Multi-head Attention. Mỗi một nhánh của input là một đầu của attention. Ở nhánh này ta thực hiện Scale dot production và output là các matrix attention.

Sau khi thu được 3 matrix attention ở đầu ra chúng ta sẽ concatenate các matrix này theo các cột để thu được ma trận tổng hợp multi-head matrix có chiều cao trùng với chiều cao của ma trận input.

$\text{MultiHead}(\mathbf{Q, K, V}) = \text{concatenate}(head_1, head_2,...,head_h)\mathbf{W_0}$ Ở đây $head_i = \text{Attention}(\mathbf{Q_i, K_i, V_i})$

Để trả về output có cùng kích thước với ma trận input chúng ta chỉ cần nhân với ma trận $\mathbf{W_0}$ chiều rộng bằng với chiều rộng của ma trận input.

3.3. Quá trình encoder và decoder

Như vậy kết thúc quá trình trên là chúng ta đã hoàn thành sub-layer thứ nhất của Transformer là multi-head Attention layer. Ở sub-layer thứ 2 chúng ta sẽ đi qua các kết nối fully connected và trả ra kết quả ở đầu ra có shape trùng với input. Mục đích là để chúng ta có thể lặp lại các block này Nx lần.

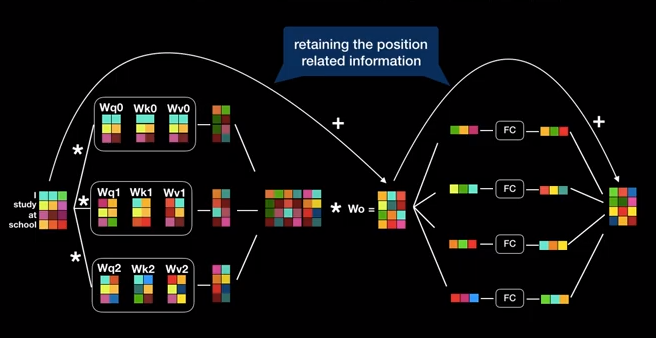
Hình 9: Sơ đồ của 1 block layer áp dụng multi-head attention layer.

Sau các biến đổi backpropagation chúng ta thường mất đi thông tin về vị trí của từ. Do đó chúng ta sẽ áp dụng một residual connection để cập nhật thông tin trước đó vào output. Cách làm này như mình đã đề cập có ý tưởng tương tự như resnet trong CNN. Để quá trình training là ổn định chúng ta sẽ áp dụng thêm một layer Normalization nữa ngay sau phép cộng.

Nếu lặp lại block layer trên 6 lần và kí hiệu chúng là một encoder. Chúng ta có thể đơn giản hóa đồ thị của quá trình encoder như bên dưới.

Hình 10: Sơ đồ quá trình encoder với 6-layer của transformer.

Quá trình decoder cũng hoàn toàn tương tự như encoder ngoại trừ lưu ý:

Quá trình decoder sẽ tạo từ theo tuần tự từ trái qua phải tại mỗi bước thời gian.
Chúng ta phải khởi tạo giá trị cho step đầu tiên (chính là thẻ <start> ở thời điểm bắt đầu). Đây có thể coi là giá trị chim mồi để decoder hoạt động. Quá trình này sẽ dừng lại khi gặp thẻ <end> để đánh dấu đã kết thúc câu dịch.
Ở mỗi một block layer của decoder chúng ta sẽ phải thêm ma trận cuối cùng của encoder như một input của multi-head attention (bạn đọc có thể xem lại hình 3).
Thêm một layer Masked Multi-head Attention sub-layer ở đầu tiên ở mỗi block layer. Layer này không có gì khác so với Multi-head Attention ngoại trừ không tính đến attention của những từ trong tương lai.

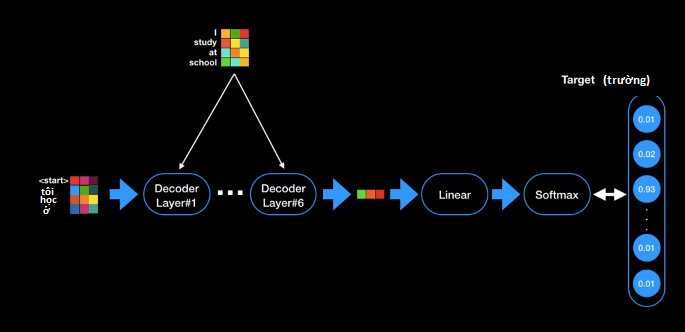
Hình 11: Quá trình biến đổi giá trị input thành các giá trị output.

Như hình 11 chúng ta thấy ở mỗi bước thời gian $t$ decoder sẽ nhận giá trị đầu vào là final-output từ encoder, input của từ ở vị trí thứ $t-1$ ở decoder (đây là giá trị được dự báo ở bước thời gian thứ $t-1$ của model). Sau khi đi qua 6 block layers của decoder model sẽ trả ra một vector đại diện cho từ được dự báo. Hàm linear kết hợp với softmax được sử dụng để tính ra giá trị phân phối xác xuất của từ mục tiêu. Để nâng cao accuracy và BLEU score (tôi sẽ giải thích chỉ số này ở mục 4) thì tác giả trong bài báo gốc có nói sử dụng kĩ thuật label smoothing tại ngưỡng label $\epsilon_{ls} = 0.1$ nhằm giảm các label tại vị trí mục tiêu xuống nhỏ hơn 1 và các vị trí khác lớn hơn 0. Việc này gây ảnh hưởng tới sự không chắc chắn của model nhưng có tác dụng trong gia tăng accuracy bởi trên thực tế 1 câu có thể có nhiều cách dịch khác nhau. Chẳng hạn như I study at school có thể dịch nhiều nghĩa như tôi học ở trường hoặc tôi nghiên cứu ở trường.

4. BLEU score

Mục này tôi chỉ giới thiệu về chỉ số BLEU score một metric chuyên biệt đánh giá các thuật toán dịch máy. BLUE là viết tắt của cụm từ Bilingual Evaluation Understudy có ý nghĩa là chỉ số giá hệ thống song ngữ. Lý do tại sao chúng ta lại lựa chọn chúng?

Để đo lường các tác vụ dịch máy hoàn toàn không đơn giản như các bài toán phân loại khác bởi ở các bài toán phân loại chúng ta đã có sẵn ground truth cho một quan sát đầu ra và ground truth này là duy nhất và cố định. Tuy nhiên đối với dịch máy, một câu input có thể có nhiều bản dịch khác nhau. Do đó không thể sử dụng nhãn duy nhất để so khớp như precision hoặc recall được. Xin phép được lấy ví dụ từ wiki về BLEU score.

Giả sử chúng ta có câu input từ tiếng Pháp là: Le chat est sur le tapis.

Đối với câu trên có 2 bản dịch tương ứng là:

Bản dịch 1: The cat is on the mat.
Bản dịch 2: There is a cat on the mat.

Giả sử bản dịch Machine Translation (viết tắt là MT) hơi đặc biệt khi gồm 7 từ the: the the the the the the the.

Nếu sử dụng precision làm thước đo, chúng ta sẽ đếm các từ xuất hiện trong MT mà xuất hiện trong toàn bộ các bản dịch (bao gồm cả 1 và 2) chia cho độ dài của MT. Như vậy sẽ có tổng cộng 7 lần từ the xuất hiện đồng thời trong các bản dịch và MT. Do đó:

\[\text{precision} = \frac{\text{total right predict}}{\text{length output}} = \frac{7}{7} = 1\]

Bản dịch trên là không tốt nhưng sử dụng precision đã đưa ra một điểm số cao cho nó nên không phù hợp để đo chất lượng thuật toán. Một cách tự nhiên hơn là chúng ta sẽ tinh chỉnh score bằng cách giới hạn cận trên của một từ được phép xuất hiện trong MT bằng cách đếm số lần xuất hiện nhiều nhất của nó trong mỗi bản dịch. Như vậy từ the được tính nhiều nhất là 2 lần bằng với số lần xuất hiện trong bản dịch 1. Khi đó điểm precision đã được modified sẽ là $\frac{2}{7}$ và có vẻ điểm này đã hợp lý hơn.

Một khía cạnh khác, để đánh giá bản dịch tốt hơn, chúng ta muốn xem sự xuất hiện của các từ theo cặp để đo được bối cảnh của từ. Để dễ hình dùng tôi sẽ thay đổi câu dịch MT sang: the cat the cat on the mat. Với câu trên chúng ta sẽ có các cặp từ đôi {the cat, cat the, cat on, on the, the mat}. Thống kê tần suất của các cặp từ trong MT (chỉ số count) và tần suất xuất hiện của chúng trong các bản dịch (chỉ số count clip) ta được bảng bên dưới:

Bigram	Count	Count clip
the cat	2	1
cat the	1	0
cat on	1	1
on the	1	1
the mat	1	1

Bảng 1: Thống kê count và count_clip của các bigram. Chỉ số count là tần suất xuất hiện của cặp từ trong MT. Chỉ số count_clip là tần suất xuất hiện của cặp từ trong các bản dịch.

Như vậy lấy tổng tần suất của cặp từ trong bản dịch chia cho tổng tần suất trong MT của các cặp bigram ta thu được precision là:

\[precision = \frac{1+1+1+1}{2+1+1+1+1} = \frac{2}{3}\]

Theo phương pháp tính precision như trên chúng ta sẽ khắc phục được hạn chế đó là các từ xuất hiện nhiều trong bản dịch như the cat do lỗi lặp từ của mô hình sẽ làm giảm precision.

Sau các ví dụ trên bạn đọc đã hình dung được cách tính precision modified rồi chứ? Tôi xin phát biểu công thức tổng quát về tính precision modified cho n-gram (kí hiệu là $P_n$) như sau:

\[P_n = \frac{\sum_{i=1}^{C} \text{count_clip}(ngram_i)}{\sum_{i=1}^{C}\text{count}(ngram_i)}\]

Trong đó C là kích thước của các ngram thu được từ bản dịch MT, $ngram_i$ là một phần tử thuộc bộ ngram. Cách tính $\text{count}$ và $\text{count_clip}$ như thống kê trong bảng 1.

Vậy BLEU score (bilingual evaluation understudy) được tính như thế nào?

BLEU score theo như giới thiệu sẽ có tác dụng đánh giá điểm số càng cao nếu kết quả của MT là sát nghĩa với kết quả của người dịch. BLEU score sẽ được tính toán dựa trên $P_1, P_2, P_3, P_4$ theo lũy thừa cơ số tự nhiên $e$:

\[BLEU = \text{exp}(\frac{P_1 + P_2 + P_3 + P_4}{4})\]

Tuy nhiên chúng ta thấy một điểm hạn chế của BLEU score đó là đối với các câu càng ngắn thì xu hướng BLEU score sẽ càng cao. Điều này dễ hiểu vì khi câu càng ngắn thì số lượng các n_gram càng ít và đồng thời khả năng xuất hiện của chúng trong các bản dịch cũng cao hơn. Chính vì vậy chúng ta cần một chỉ số phạt độ ngắn gọi là Brevity Penalty (kí hiệu là BP).

\[\begin{equation} BP = \left\{ \begin{array}{l l} 1 \space \text{if MT_output_length > Reference_output_length} \\ \text{exp(1-MT_output_length/Reference_output_length) otherwise} \end{array} \right. \end{equation}\]

Khi đó:

\[BLEU = BP \times \text{exp}(\frac{P_1 + P_2 + P_3 + P_4}{4})\]

Hiện nay có nhiều package trên đa dạng các ngôn ngữ machine learning hỗ trợ tính BLEU score. Trên python chúng ta có thể sử dụng package nltk như sau:

from nltk.translate.bleu_score import sentence_bleu
reference = [['the', 'quick', 'brown', 'fox', 'jumped', 'over', 'the', 'lazy', 'dog']]
MT_translation = ['the', 'fast', 'brown', 'fox', 'jumped', 'over', 'the', 'sleepy', 'dog']
score = sentence_bleu(reference, MT_translation)
print(score)

Bạn đọc cũng có thể tự xây dựng cho mình hàm tính BLEU score theo công thức đã cung cấp.

5. Thực hành Attention Layer

Về code của Multi-head Attention layer đã có nhiều nguồn public trên mạng. Một trong số source khá tốt là Transformer - Kyubyoung. Vì việc code lại thuật toán khá tốn thời gian nên tôi xin giải thích các hàm trong code mẫu trên mà bạn đọc sẽ gặp.

Hàm tính scale_dot_product_attention: Hàm này sẽ trả về kết quả như ở công thức (1), khi đã biết 3 ma trận là $\mathbf{Q, K, V}$

Trước khi tính được scale dot product attention từ đầu vào là ma trận inputs, chúng ta cần tính được các ma trận $\mathbf{Q, K, V}$ thông qua hàm mask như sau:

def mask(inputs, queries=None, keys=None, type=None):
    """Masks paddings on keys or queries to inputs
    inputs: 3d tensor. (N, T_q, T_k)
    queries: 3d tensor. (N, T_q, d)
    keys: 3d tensor. (N, T_k, d)
    """
    padding_num = -2 ** 32 + 1
    if type in ("k", "key", "keys"):
        # Tọa ma trận mask
        # Dấu của tổng các dòng 
        masks = tf.sign(tf.reduce_sum(tf.abs(keys), axis=-1))  # (N, T_k)
        # Mở rộng tổng thêm 1 chiều thứ 2
        masks = tf.expand_dims(masks, 1) # (N, 1, T_k)
        # Lặp lại chiều của dấu tổng các dòng T_q lần
        masks = tf.tile(masks, [1, tf.shape(queries)[1], 1])  # (N, T_q, T_k)

        # Tạo ma trận  paddings có kích thước như inputs và các phần tử đều bằng -2^32+1
        paddings = tf.ones_like(inputs) * padding_num
        # Tại 1 vị trí bất kì. Nếu bằng 0 thì lấy từ giá trị -2^32+1, nếu sai lấy từ inputs.
        outputs = tf.where(tf.equal(masks, 0), paddings, inputs)  # (N, T_q, T_k)
    elif type in ("q", "query", "queries"):
        # Generate masks
        masks = tf.sign(tf.reduce_sum(tf.abs(queries), axis=-1))  # (N, T_q)
        masks = tf.expand_dims(masks, -1)  # (N, T_q, 1)
        masks = tf.tile(masks, [1, 1, tf.shape(keys)[1]])  # (N, T_q, T_k)

        # Apply masks to inputs
        outputs = inputs*masks
    elif type in ("f", "future", "right"):
        diag_vals = tf.ones_like(inputs[0, :, :])  # (T_q, T_k)
        tril = tf.linalg.LinearOperatorLowerTriangular(diag_vals).to_dense()  # (T_q, T_k)
        masks = tf.tile(tf.expand_dims(tril, 0), [tf.shape(inputs)[0], 1, 1])  # (N, T_q, T_k)

        paddings = tf.ones_like(masks) * padding_num
        outputs = tf.where(tf.equal(masks, 0), paddings, inputs)
    else:
        print("Check if you entered type correctly!")
    return outputs

Ví dụ về kết quả của hàm mask đối với key.

import tensorflow as tf
queries = tf.constant([[[1.],
                [2.],
                [0.]]], tf.float32) # (1, 3, 1)
keys = tf.constant([[[4.],
             [0.]]], tf.float32)  # (1, 2, 1)
inputs = tf.constant([[[4., 0.],
                       [8., 0.],
                       [0., 0.]]], tf.float32) # (1, 3, 2)
y = mask(inputs, queries, keys, "key")

with tf.Session() as sess:
    print('mask function for key: \n ', sess.run(y))

mask function for key: 
  [[[ 4.0000000e+00 -4.2949673e+09]
  [ 8.0000000e+00 -4.2949673e+09]
  [ 0.0000000e+00 -4.2949673e+09]]]

def scale_dot_product_attention(Q, K, V,
                                causality = False, dropout_rate = 0.,
                                training = True,
                                scope = 'scaled_dot_product_attention'):
    '''
    Q: Ma trận queries kích thước [N, T_q, d_k]
    K: Ma trận keys kích thước    [N, T_k, d_k]
    V: Ma trận values kích thước  [N, T_k, d_v]
    causality: Quan hệ nhân quả. Nếu True, sẽ áp dụng masking cho những giá trị tương lai mà chưa được thấy.
    dropout_rate: Tỷ lệ dropout ở fully connected, nằm trong [0,1].
    training: kiểm soát dropout_rate.
    scope: Scope tùy chọn cho `variable_scope`
    '''
    with tf.variable_scope(scope, reuse=tf.AUTO_REUSE):
        d_k = Q.get_shape().as_list()[-1]
        
        # dot products
        outputs = tf.matmul(Q, tf.transpose(K, [0, 2, 1])) # N, T_q, T_k
        # scale
        outputs /= d_k**0.5
        # key masking
        outputs = mask(outputs, Q, K, type='key')
        # causality or future binding masking
        if causality:
            outputs = mask(outputs, type="future")

        # softmax
        outputs = tf.nn.softmax(outputs)
        attention = tf.transpose(outputs, [0, 2, 1])
        tf.summary.image("attention", tf.expand_dims(attention[:1], -1))
        
        # query masking
        outputs = mask(outputs, Q, K, type="query")
        with tf.Session() as sess:
            print('Attention weight: \n', sess.run(outputs))
        # dropout
        outputs = tf.layers.dropout(outputs, rate=dropout_rate, training=training)
        # Mỗi 1 dòng của outputs là một phân phối xác xuất của attention.
        # weighted sum (context vectors)
        outputs = tf.matmul(outputs, V)  # (N, T_q, d_v)

    return outputs

Ví dụ về hàm scale_dot_product_attention

import numpy as np
import tensorflow as tf
Q = tf.reshape(tf.random.normal(np.array([6]), mean = 0, stddev = 1.0, dtype = tf.float32), (1, 3, 2)) #[N, T_q, d_k]
K = tf.reshape(tf.random.normal(np.array([6]), mean = 1, stddev = 2.0, dtype = tf.float32), (1, 3, 2)) #[N, T_k, d_k]
V = tf.reshape(tf.range(0, 6, 1, dtype = tf.float32), (1, 3, 2)) #[N, T_k, d_v]
with tf.Session() as sess:
    print('Q matrix: \n', sess.run(Q))
    print('K matrix: \n', sess.run(K))
    print('V matrix: \n', sess.run(V))
    print('Attention matrix by scale dot product: \n', sess.run(scale_dot_product_attention(Q, K, V)))

Q matrix: 
 [[[ 1.6889378 -2.1054077]
  [-1.3970122 -1.2317009]
  [-0.8323478  2.8157258]]]
K matrix: 
 [[[-0.1563865  -1.0208571 ]
  [ 1.0360996   2.7422607 ]
  [-1.2121758   0.51843137]]]
V matrix: 
 [[[0. 1.]
  [2. 3.]
  [4. 5.]]]
Attention weight: 
 [[[0.15708944 0.2708901  0.5720205 ]
  [0.6267046  0.33209655 0.04119889]
  [0.27744606 0.47145858 0.25109527]]]
Attention matrix by scale dot product: 
 [[[0.2910742  1.2910742 ]
  [3.4131784  4.4131784 ]
  [0.90950227 1.9095023 ]]]

Hàm multi-head attention: sẽ được tính toán dựa trên những scale_dot_product_attention.

def multihead_attention(queries, keys, values,
                        num_heads=8,
                        dropout_rate=0,
                        training=True,
                        causality=False,
                        scope="multihead_attention"):
    d_model = queries.get_shape().as_list()[-1]
    with tf.variable_scope(scope, reuse=tf.AUTO_REUSE):
        # Linear projections
        Q = tf.layers.dense(queries, d_model, use_bias=False)  # (N, T_q, d_model)
        K = tf.layers.dense(keys, d_model, use_bias=False)  # (N, T_k, d_model)
        V = tf.layers.dense(values, d_model, use_bias=False)  # (N, T_k, d_model)

        # Chia các ma trận Q, K, V thành h phần bằng nhau. Mỗi phần có kích thước (N, T_{q or k}, d_model/h) được coi như là input
        # để biến đổi một head trong ma multi-head attention.
        
        Q_ = tf.concat(tf.split(Q, num_heads, axis=2), axis=0)  # (h*N, T_q, d_model/h)
        K_ = tf.concat(tf.split(K, num_heads, axis=2), axis=0)  # (h*N, T_k, d_model/h)
        V_ = tf.concat(tf.split(V, num_heads, axis=2), axis=0)  # (h*N, T_k, d_model/h)

        # Attention
        outputs = scaled_dot_product_attention(Q_, K_, V_, causality, dropout_rate, training) # (h*N, T_q, d_model/h)

        # Thực hiện concatenate các head như hình 9
        outputs = tf.concat(tf.split(outputs, num_heads, axis=0), axis=2)  # (N, T_q, d_model)

        # Residual connection: Cộng thêm input vào output như hình 9.
        outputs += queries

        # Normalize: Chuẩn hóa để tăng tốc độ của thuật toán training.
        outputs = ln(outputs)

    return outputs

Điểm mấu chốt trong code của multi-head đó là ta phải chia lại kích thước của các ma trận $\mathbf{Q, K, V}$ để tạo thành $h$ phép biến đổi trên các ma trận con $\mathbf{Q’, K’, V’}$ có chung kích thước. Mỗi phép biến đổi này sẽ là một head của multi-attention.

Về kết quả của thuật toán trong bài báo Attention layer is all you need cho thấy thuật toán có độ chính xác cao hơn so với các lớp model dịch máy khác và đồng thời có chi phí tính toán thấp hơn. Cụ thể như bảng sau:

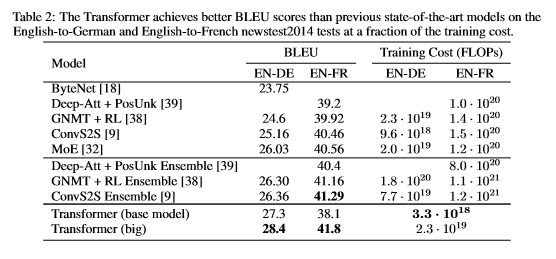
Hình 12: Kết quả của thuật toán transformer.

6. Tổng kết

Như vậy sau bài hướng dẫn này các bạn đã biết được:

Cấu trúc 2 phase encoder và decoder của một thuật toán dịch máy.
Kiến trúc mạng của transformer.
Biến đổi scale dot production attention để tìm ra ma trận attention weight.
Phương pháp thực hiện multi-head attention layers dựa trên từng single-head.
Metric đo lường mức độ chính xác của model dịch máy thông qua BLEU score (bilanguage evaluation understudy).

Đến đây tôi xin kết thúc phần lý giải về thuật toán transformer và attention ứng dụng trong dịch máy. Bài viết được thực hiện dựa trên rất nhiều các tài liệu tham khảo. Tôi xin gửi lời cảm ơn chân thành tới các tác giả bài viết gốc, các vlog trên mạng đã chia sẻ kiến thức và hiểu biết của mình về model này. Bài viết có thể còn nhiều hạn chế. Rất mong đóng góp từ phía độc giả.