Bài 19 - Mô hình ARIMA trong time series
12 Dec 2019 - phamdinhkhanh1. Giới thiệu về chuỗi thời gian
Dự báo chuỗi thời gian là một lớp mô hình quan trọng trong thống kê, kinh tế lượng và machine learning. Sở dĩ chúng ta gọi lớp mô hình này là chuỗi thời gian (time series) là vì mô hình được áp dụng trên các chuỗi đặc thù có yếu tố thời gian. Một mô hình chuỗi thời gian thường dự báo dựa trên giả định rằng các qui luật trong quá khứ sẽ lặp lại ở tương lai. Do đó xây dựng mô hình chuỗi thời gian là chúng ta đang mô hình hóa mối quan hệ trong quá khứ giữa biến độc lập (biến đầu vào) và biến phụ thuộc (biến mục tiêu). Dựa vào mối quan hệ này để dự đoán giá trị trong tương lai của biến phụ thuộc.
Do là dữ liệu chịu ảnh hưởng bởi tính chất thời gian nên chuỗi thời gian thường xuất hiện những qui luật đặc trưng như : yếu tố chu kỳ, mùa vụ và yếu tố xu hướng. Đây là những đặc trưng thường thấy và xuất hiện ở hầu hết các chuỗi thời gian.
- Yếu tố chu kỳ, mùa vụ là những đặc tính lặp lại theo chu kỳ. Ví dụ như nhiệt độ trung bình các tháng trong năm sẽ chịu ảnh hưởng bởi các mùa xuân, hạ, thu, đông. Hay xuất nhập khẩu của một quốc gia thường có chu kỳ theo các quí.
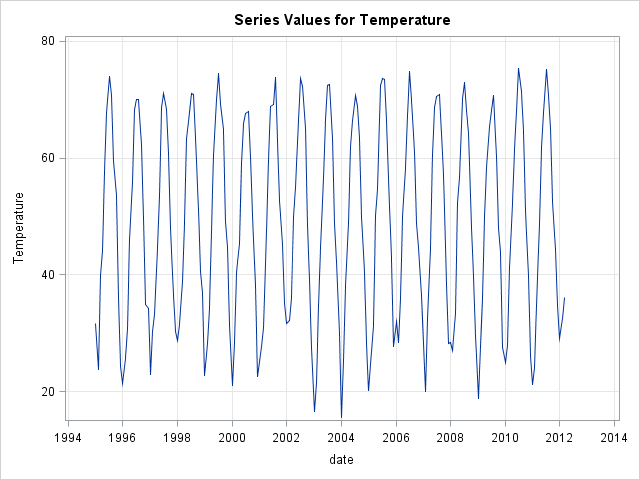
Hình 1: Đồ thị về chuỗi nhiệt độ trung bình theo tháng thể hiện yếu tố mùa vụ.
- Yếu tố xu hướng (trend) thể hiện đà tăng hoặc giảm của chuỗi trong tương lai. Chẳng hạn như lạm phát là xu hướng chung của các nền kinh tế, do đó giá cả trung bình của giỏ hàng hóa cơ sở hay còn gọi là chỉ số CPI luôn có xu hướng tăng và xu hướng tăng này đại diện cho sự mất giá của đồng tiền.
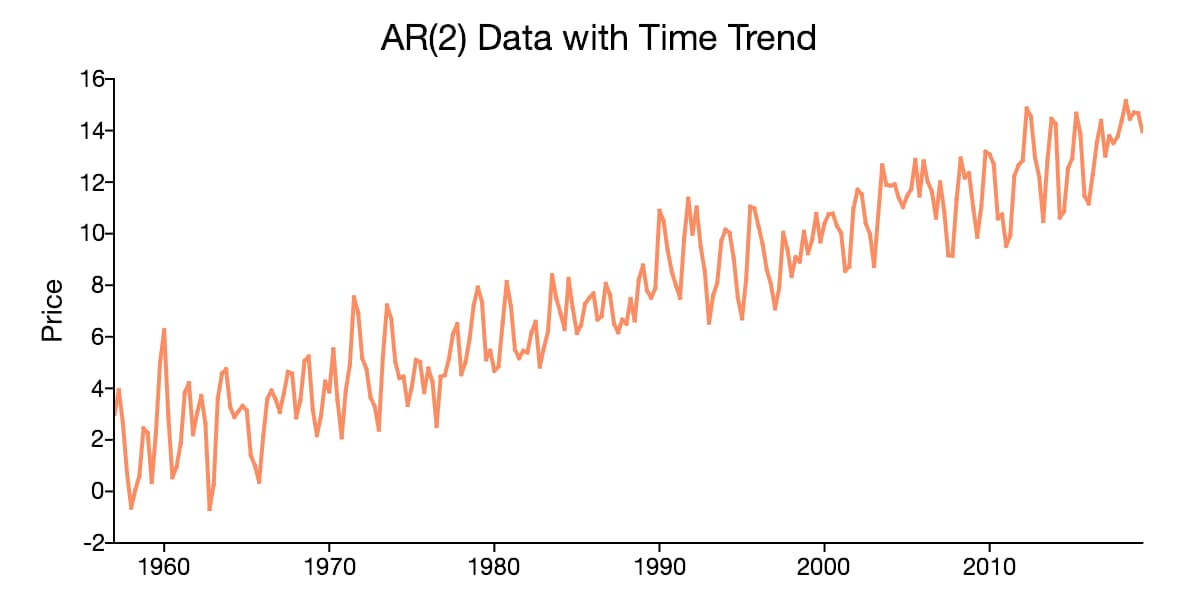
Hình 2: Đồ thị về yếu tố xu hướng trong chuỗi thời gian của chuỗi giá.
Các dự báo chuỗi thời gian có tính ứng dụng cao và được sử dụng rất nhiều lĩnh vực như tài chính ngân hàng, chứng khoán, bảo hiểm, thương mại điện tử, marketing, quản lý chính sách. Bên dưới là một số ứng dụng của dự báo chuỗi thời gian:
- Dự báo nhu cầu thị trường để lập kết hoạch sản xuất kinh doanh cho hãng.
- Dự báo lợi suất tài sản tài chính, tỷ giá, giá cả hàng hóa phái sinh để thực hiện trading hiệu quả trong market risk.
- Dự báo giá chứng khoán, các chuỗi lợi suất danh mục để quản trị danh mục đầu tư.
- Dự báo giá bitcoin, giá dầu mỏ, giá gas,…
- Dự báo nhiệt độ, lượng mưa để lập kế hoạch sản xuất nông, lâm, ngư nghiệp.
- Dự báo tác động của các nhân tố vĩ mô như lãi suất, cung tiền, đầu tư trực tiếp nước ngoài, chi tiêu chính phủ, lạm phát,… tác động lên tăng trưởng GDP để điều hành nền kinh tế.
Vai trò của chuỗi thời gian rất quan trọng đối với nền kinh tế và hoạt động của doanh nghiệp nên trong machine learning và thống kê có những ngành học nghiên cứu chuyên sâu về chuỗi thời gian như kinh tế lượng, định giá tài sản tài chính.
Khác với các mô hình dự báo thông thường trong machine learning, các mô hình trong dự báo chuỗi thời gian trong kinh tế lượng có những đặc trưng rất riêng. Đòi hỏi phải tuân thủ nghiêm ngặt các điều kiện về chuỗi dừng, nhiễu trắng và tự tương quan. Có rất nhiều lớp mô hình chuỗi thời gian khác nhau và mỗi một lớp mô hình sẽ có một tiêu chuẩn áp dụng cụ thể. Chúng ta có thể liệt kê một số mô hình phổ biến:
- Mô hình ARIMA: Dựa trên giả thuyết chuỗi dừng và phương sai sai số không đổi. Mô hình sử dụng đầu vào chính là những tín hiệu quá khứ của chuỗi được dự báo để dự báo nó. Các tín hiệu đó bao gồm: chuỗi tự hồi qui AR (auto regression) và chuỗi trung bình trượt MA (moving average). Hầu hết các chuỗi thời gian sẽ có xu hướng tăng hoặc giảm theo thời gian, do đó yếu tố chuỗi dừng thường không đạt được. Trong trường hợp chuỗi không dừng thì ta sẽ cần biến đổi sang chuỗi dừng bằng sai phân. Khi đó tham số đặc trưng của mô hình sẽ có thêm thành phần bậc của sai phân d và mô hình được đặc tả bởi 3 tham số ARIMA(p, d, q).
- Mô hình SARIMA: Về bản chất đây là mô hình ARIMA nhưng được điều chỉnh đặc biệt để áp dụng cho những chuỗi thời gian có yếu tố mùa vụ. Như chúng ta đã biết về bản chất ARIMA chính là mô hình hồi qui tuyến tính nhưng mối quan hệ tuyến tính thường không giải thích tốt chuỗi trong trường hợp chuỗi xuất hiện yếu tố mùa vụ. Chính vì thế, bằng cách tìm ra chu kì của qui luật mùa vụ và loại bỏ nó khỏi chuỗi ta sẽ dễ dàng hồi qui mô hình theo phương pháp ARIMA.
- Mô hình ARIMAX: Là một dạng mở rộng của model ARIMA. Mô hình cũng dựa trên giải định về mối quan hệ tuyến tính giữa giá trị và phương sai trong quá khứ với giá trị hiện tại và sử dụng phương trình hồi qui tuyến tính được suy ra từ mối quan hệ trong quá khứ nhằm dự báo tương lai. Mô hình sẽ có thêm một vài biến độc lập khác và cũng được xem như một mô hình hồi qui động (hoặc một số tài liệu tiếng việt gọi là mô hình hồi qui động thái). Về bản chất ARIMAX tương ứng với một mô hình hồi qui đa biến nhưng chiếm lợi thế trong dự báo nhờ xem xét đến yếu tố tự tương quan được biểu diễn trong phần dư của mô hình. Nhờ đó cải thiện độ chính xác.
- Mô hình GARCH: Các giả thuyết về chuỗi dừng và phương sai sai số không đổi đều không dễ đạt được trong thực tế. Trái lại phương sai sai số biến đổi rất dễ xảy ra đối với các chuỗi tài chính, kinh tế bởi thường có những sự kiện không mong đợi và cú sốc kinh tế không lường trước khiến biến động phương sai của chuỗi thay đổi. Trong trường hợp đó nếu áp dụng ARIMA thì thường không mang lại hiệu quả cao cho mô hình. Các nhà kinh tế lượng và thống kê học đã nghĩ đến một lớp mô hình mà có thể dự báo được phương sai để kiểm soát các thay đổi không mong đợi. Dựa trên qui luật của phương sai, kết quả dự báo chuỗi sẽ tốt hơn so với trước đó.
2. Mô hình ARIMA
Hiện tại cả R và python đều support xây dựng các mô hình chuỗi thời gian ARIMA, SARIMA, ARIMAX, GARCH,…. Trên R chúng ta có thể sử dụng các packages như forecast và lmtest để xây dựng các mô hình này khá dễ dàng. Đối với thống kê và các mô hình chuỗi thời gian R đang support tốt hơn python. Một lý do đó là các nhà thống kê và kinh tế lượng ưa chuộng sử dụng R hơn. Hướng dẫn xây dựng mô hình ARIMA trên R các bạn có thể xem tại ARIMA turtorial và GARCH time series model.
Bài hôm nay tôi sẽ hướng dẫn các bạn sử dụng python để xây dựng các model ARIMA. Nhưng trước tiên chúng ta cần tìm hiểu lý thuyết của mô hình trước khi đi vào phần thực hành ở mục 3 và 4.
2.1. Lý thuyết mô hình ARIMA
Lý thuyết: Chúng ta biết rằng hầu hết các chuỗi thời gian đều có sự tương quan giữa giá trị trong quá khứ đến giá trị hiện tại. Mức độ tương quan càng lớn khi chuỗi càng gần thời điểm hiện tại. Chính vì thể mô hình ARIMA sẽ tìm cách đưa vào các biến trễ nhằm tạo ra một mô hình dự báo fitting tốt hơn giá trị của chuỗi.
ARIMA model là viết tắt của cụm từ Autoregressive Intergrated Moving Average. Mô hình sẽ biểu diễn phương trình hồi qui tuyến tính đa biến (multiple linear regression) của các biến đầu vào (còn gọi là biến phụ thuộc trong thống kê) là 2 thành phần chính:
- Auto regression: Kí hiệu là AR. Đây là thành phần tự hồi qui bao gồm tợp hợp các độ trễ của biến hiện tại. Độ trễ bậc $p$ chính là giá trị lùi về quá khứ $p$ bước thời gian của chuỗi. Độ trễ dài hoặc ngắn trong quá trình AR phụ thuộc vào tham số trễ $p$. Cụ thể, quá trình $\text{AR}(p)$ của chuỗi $x_{t}$ được biểu diễn như bên dưới:
- Moving average: Qúa trình trung bình trượt được hiểu là quá trình dịch chuyển hoặc thay đổi giá trị trung bình của chuổi theo thời gian. Do chuỗi của chúng ta được giả định là dừng nên quá trình thay đổi trung bình dường như là một chuỗi nhiễu trắng. Qúa trình moving average sẽ tìm mối liên hệ về mặt tuyến tính giữa các phần tử ngẫu nhiên $\epsilon_{t}$ (stochastic term). Chuỗi này phải là một chuỗi nhiễu trắng thỏa mãn các tính chất:
Vế (1) có nghĩa rằng kì vọng của chuỗi bằng 0 để đảm bảo chuỗi dừng không có sự thay đổi về trung bình theo thời gian. Vế (2) là phương sai của chuỗi không đổi. Do kì vọng và phương sai không đổi nên chúng ta gọi phân phối của nhiễu trắng là phân phối xác định (identical distribution) và được kí hiệu là $\epsilon_{t}∼\text{WN}(0,\sigma^2)$. Nhiễu trắng là một thành phần ngẫu nhiên thể hiện cho yếu tố không thể dự báo của model và không có tính qui luật. Qúa trình trung bình trượt được biểu diễn theo nhiễu trắng như sau:
\[\text{MA}(q) = \mu+\sum_{i=1}^{q} \theta_i\epsilon_{t-i}\]Qúa trình này có thể được biểu diễn theo dịch chuyển trễ - backshift operator $B$ như sau:
\[\text{MA}(q) = \mu+(1+\theta_1 B + \dots + \theta_q B^{q})\epsilon_{t}\]Như vậy bạn đọc đã hình dung ra moving average là gì rồi chứ? Về mặt ý tưởng thì đó chính là quá trình hồi qui tuyến tính của giá trị hiện tại theo các giá trị hiện tại và quá khứ của sai số nhiễu trắng (white noise error term) đại diện cho các yếu tố shock ngẫu nhiên, những sự thay đổi không lường trước và giải thích bởi mô hình.
-
Intergrated: Là quá trình đồng tích hợp hoặc lấy sai phân. Yêu cầu chung của các thuật toán trong time series là chuỗi phải đảm bảo tính dừng. Hầu hết các chuỗi đều tăng hoặc giảm theo thời gian. Do đó yếu tố tương quan giữa chúng chưa chắc là thực sự mà là do chúng cùng tương quan theo thời gian. Khi biến đổi sang chuỗi dừng, các nhân tố ảnh hưởng thời gian được loại bỏ và chuỗi sẽ dễ dự báo hơn. Để tạo thành chuỗi dừng, một phương pháp đơn giản nhất là chúng ta sẽ lấy sai phân. Một số chuỗi tài chính còn qui đổi sang logarit hoặc lợi suất. Bậc của sai phân để tạo thành chuỗi dừng còn gọi là bậc của quá trình đồng tích hợp (order of intergration). Qúa trình sai phân bậc $d$ của chuỗi được thực hiện như sau:
-
Sai phân bậc 1: \(\text{I}(1) = \Delta(x_t) = x_{t} - x_{t-1}\)
-
Sai phân bậc d: \(\text{I}(d) = \Delta^{d}(x_t) = \underbrace{\Delta(\Delta(\dots \Delta(x_t)))}_{\text{d times}}\)
-
Thông thường chuỗi sẽ dừng sau quá trình đồng tích hợp $\text{I}(0)$ hoặc $\text{I}(1)$. Rất ít chuỗi chúng ta phải lấy tới sai phân bậc 2. Một số trường hợp chúng ta sẽ cần biến đổi logarit hoặc căn bậc 2 để tạo thành chuỗi dừng. Phương trình hồi qui ARIMA(p, d, q) có thể được biểu diễn dưới dạng:
\[\Delta x_{t} = \phi_{1} \Delta x_{t-1}+\phi_{2} \Delta x_{t-2}+...+\phi_{p}\Delta x_{t-p}+ \theta_{1}\epsilon_{t-1}+\theta_{2}\epsilon_{t-2}+...+\theta_{q}\epsilon_{t-q}\]Trong đó $\Delta x_t$ là giá trị sai phân bậc $d$ và $\epsilon_t$ là các chuỗi nhiễu trắng.
Như vậy về tổng quát thì ARIMA là mô hình kết hợp của 2 quá trình tự hồi qui và trung bình trượt. Dữ liệu trong quá khứ sẽ được sử dụng để dự báo dữ liệu trong tương lai. Trước khi huấn luyện mô hình, cần chuyển hóa chuỗi sang chuỗi dừng bằng cách lấy sai phân bậc 1 hoặc logarit. Ngoài ra mô hình cũng cần tuân thủ điều kiện ngặt về sai số không có hiện tượng tự tương quan và phần dư là nhiễu trắng. Đó là lý thuyết của kinh tế lượng. Còn theo trường phái machine learning thì tôi chỉ cần quan tâm đến làm sao để lựa chọn một mô hình có sai số dự báo là nhỏ nhất. Tiếp theo chúng ta sẽ sử dụng package vnquant, một package được tôi viết để hỗ trợ cộng đồng khai thác dữ liệu chứng khoán thuận tiện hơn.
3. Ứng dụng vnquant trong thu thập dữ liệu.
3.1. Thu thập dữ liệu
Hiện tại package vnquant đã cho phép chúng ta thu thập được hầu hết mã chứng khoán trên thị trường chứng khoán Việt Nam, ở phiên bản R (package VNDS) còn thu thập được báo cáo tài chính và dòng tiền của doanh nghiệp. Ngoài ra vnquant còn hỗ trợ vẽ biểu đồ nến theo thời gian và kết hợp giữa giá và khối lượng giao dịch. Đây là một package mà mình nghĩ là rất hữu ích đối với các bạn làm trong lĩnh vực quant tại Việt Nam. Để cài đặt package này bạn làm như hướng dẫn trong phần read me nhé.
Bây giờ chúng ta sẽ cùng lấy dữ liệu chỉ số VNINDEX 30 thông qua package vnquant nào.
1
2
3
4
5
6
7
8
9
10
from vnquant.DataLoader import DataLoader
loader = DataLoader(symbols="VN30",
start="2019-01-01",
end="2019-12-09",
minimal=False,
data_source="vnd")
data = loader.download()
data.head()
1
2
2019-12-12 04:22:07,057 : INFO : NumExpr defaulting to 2 threads.
2019-12-12 04:22:07,076 : INFO : data VN30 from 2019-01-01 to 2019-12-09 have already cloned!
| Attributes | change_perc1 | change_perc2 | open | high | low | close | avg | volume_match | volume_reconcile | volume |
|---|---|---|---|---|---|---|---|---|---|---|
| Symbols | VN30 | VN30 | VN30 | VN30 | VN30 | VN30 | VN30 | VN30 | VN30 | VN30 |
| date | ||||||||||
| 2019-01-02 | 0.00 | 0.000000 | 855.01 | 864.64 | 852.79 | 855.66 | 855.66 | 37199310.0 | 3099070.0 | 40298380.0 |
| 2019-01-03 | -16.87 | 0.019716 | 855.20 | 856.21 | 834.81 | 838.79 | 838.79 | 55933762.0 | 5880342.0 | 61814104.0 |
| 2019-01-04 | 1.38 | 0.001645 | 836.60 | 842.05 | 821.83 | 840.17 | 840.17 | 41706643.0 | 4266803.0 | 45973446.0 |
| 2019-01-07 | 11.24 | 0.013378 | 843.95 | 858.69 | 843.95 | 851.41 | 851.41 | 35905579.0 | 5233979.0 | 41139558.0 |
| 2019-01-08 | -5.98 | 0.007024 | 851.20 | 852.92 | 841.86 | 845.43 | 845.43 | 33310330.0 | 5386790.0 | 38697120.0 |
Sử dụng hàm visualization trên chính vnquant để visualize dữ liệu lịch sử giá và khối lượng giao dịch.
1
2
3
4
5
from vnquant import Plot
Plot._vnquant_candle_stick(data = data,
title='VNIndex 30 from 2019-01-02 to 2019-12-09',
ylab='Date', xlab='Price',
show_vol=True)
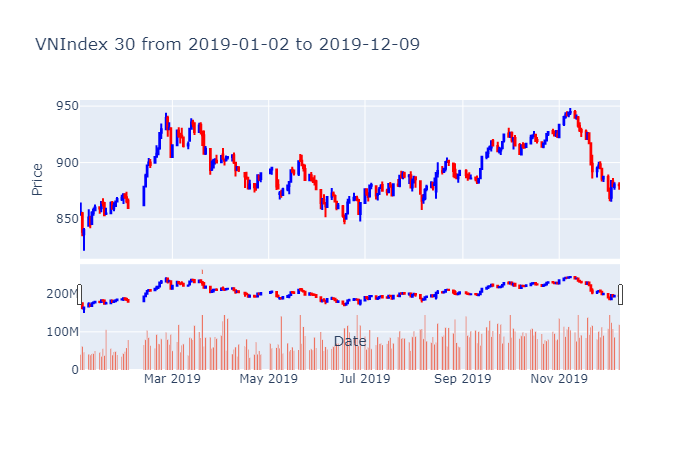
Nhận xét, năm 2019 là một năm thị trường chứng khoán có nhiều thăng trầm biến động khi chỉ số có lúc vượt ngưỡng 950 nhưng có những giai đoạn hạ xuống thấp hơn 850 điểm. Tuy nhiên chưa thể phục hồi lại ngưỡng đỉnh cao trên 1000 điểm của năm 2018.
3.2. Khởi tạo chuỗi lợi suất và khảo sát dữ liệu
Để thuận tiện cho việc xây dựng mô hình ARIMA ta sẽ chuyển chuỗi giá close sang chuỗi dừng bằng cách lấy lợi suất theo công thức sai phân bậc 1 của logarit như bên dưới:
\[r_t = \log(\frac{x_t}{x_{t-1}})\]Mục tiêu của mô hình sẽ là dự báo chuỗi $r_t$. Từ chuỗi $r_t$ ta có thể dễ dàng biến đổi ngược lại thành giá đóng cửa của chuỗi VnIndex 30.
Hàm data.shift(1) sẽ giúp ta lấy trễ bậc 1 của chuỗi giá close. Công thức tính toán lợi suất như sau:
1
2
3
import numpy as np
# Tính chuỗi return
r_t = np.log(data['close']/data['close'].shift(1)).values[:, 0]
Fill giá trị np.nan bằng trung bình chuỗi.
1
2
3
mean = np.nanmean(r_t)
r_t[0]=mean
r_t[:5]
1
array([ 0.00012009, -0.01991272, 0.00164388, 0.01328955, -0.00704843])
Các biểu đồ:
- Biểu đồ lợi suất:
Để hiểu rõ hơn về xu hướng, biến động, ta hãy cùng vẽ biểu đồ chuỗi lợi suất $r_t$.
1
2
3
4
5
6
7
8
9
import matplotlib.pyplot as plt
plt.figure(figsize=(16, 4))
plt.plot(np.arange(r_t.shape[0]), r_t, '-o')
plt.axhline(y=mean, label='mean return', c='red')
plt.title('Return rate according to date')
plt.xlabel('Date Order')
plt.ylabel('Return Rate')
plt.legend()
plt.show()
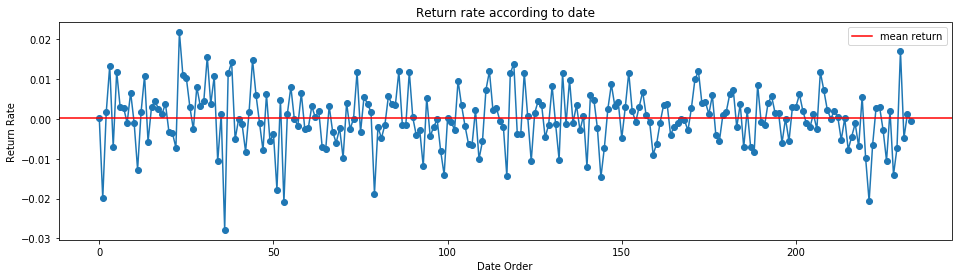
Nhận xét: Biểu đồ chuỗi lợi suất cho thấy nó là một biến động ngẫu nhiên dạng nhiễu trắng, có trung bình gần như bằng 0 và phương sai không đổi.
- Quan hệ tuyến tính $r_t$ và $r_{t-1}$
Ta có thể vẽ biểu đồ biểu diễn chuỗi $r_t$ dựa trên chuỗi $r_{t-1}$ để xem chúng có quan hệ tuyến tính hay ngẫu nhiên.
1
2
3
4
5
6
7
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 8))
plt.scatter(x=r_t[1:], y=r_t[:-1])
plt.title('Return rate vs Lag order 1 according to date')
plt.xlabel('r(t-1)')
plt.ylabel('r(t)')
plt.show()
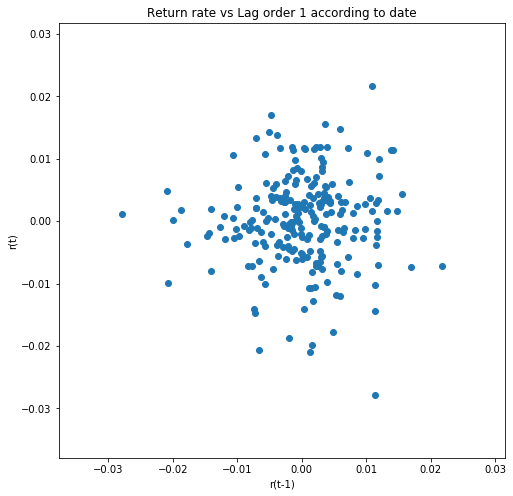
Đồ thị cho thấy 2 chuỗi $r_t$ và $r_{t-1}$ không có mối quan hệ tương quan. Biểu đồ của chúng là một tợp hợp các điểm không tuân theo một trend cụ thể.
- Phân phối xác suất:
Ta hãy cũng khảo sát qua biểu đồ phân phối xác suất của chuỗi lợi suất.
1
2
3
4
5
6
7
8
9
import seaborn as sns
plt.figure(figsize = (8, 6))
sns.distplot(r_t, bins = 20)
plt.axvline(x=mean, label='mean return', c='red')
plt.title('Distribution return of VnIndex30')
plt.legend()
plt.xlabel('return rate')
plt.ylabel('frequency')
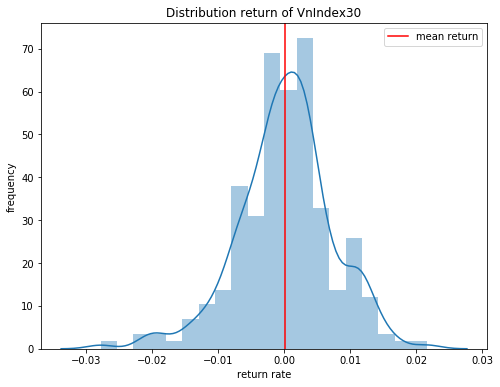
Từ biểu đồ phân phối lợi suất ta nhận thấy chuỗi phân phối lợi suất dường như có dạng phân phối chuẩn và có kì vọng bằng 0. Chúng ta có thể kiểm định phân phối chuẩn thông qua biểu đồ qqplot (quantiles quantiles plot).
- Biểu đồ Quantile-Quantile plot: Là một trong những phương pháp kiểm định non-parametric trong thống kê để kiểm định một đại lượng có tuân theo một phân phối nào đó dựa trên so sánh các hình dạng của 2 phân phối xác suất thực nghiệm (emperical) và lý thuyết (theoretical). Ví dụ: Ta giả định rằng $r_t$ là một chuỗi phân phối chuẩn. Chuỗi $r_t$ khi đó được gọi là chuỗi thực nghiệm. Từ các tham số của chuỗi như trung bình $\mu$ và phương sai $\sigma^2$ ta sẽ xác định được một phân phối chuẩn $N(\mu, \sigma^2)$, đây chính là phân phối xác suất lý thuyết. Đầu tiên chuỗi $r_t$ sẽ được sắp xếp theo thứ tự tăng dần. Sau đó ứng với mỗi một điểm dữ liệu ta sẽ xác định xem nó thuộc khoảng ngũ phân vị nào của phân phối xác suất lý thuyết. Gía trị điểm phân chia xác suất của các khoảng ngũ phân vị lần lượt là $[0.2, 0.4, 0.6, 0.8]$. Như vậy nếu một điểm dữ liệu $r_i$ thỏa mãn:
thì nó sẽ nằm trong khoảng ngũ phân vị thứ 2. Biểu đồ qqplot sẽ biểu diễn các điểm có tọa độ $(x, y)$ sao cho giá trị $x$ chính là khoảng ngũ phân vị theo phân phối chuẩn và giá trị $y$ chính là giá trị thực nghiệm. Từ biểu đồ ta kết luận 2 chuỗi có phân phối tương tự nhau nếu như các điểm trên đồ thì nằm trên một đường thẳng. Khi đó $r_t$ có thể được coi như là một phân phối chuẩn. Cách kiểm định phân phối chuẩn dựa trên biểu đồ qqplot được sử dụng khá phổ biến nhưng nó có một nhược điểm là không cung cấp một tiêu chuẩn xác định của việc chấp nhận/bác bỏ giả thuyết. Để vẽ biểu đồ qqplot ta có thể làm theo 2 cách khác nhau.
Cách 1: Sử dụng trực tiếp hàm sm.qqplot().
1
2
3
import statsmodels.api as sm
sm.qqplot(r_t)
plt.show()
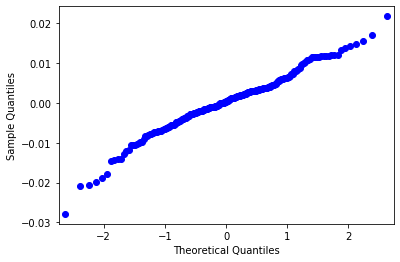
Cách 2: Tính ra chuỗi lý thuyết và vẽ đồ thị Chúng ta cũng có thể vẽ biểu đồ qqplot bằng cách tính ra trực tiếp giá trị phân phối thực nhiệm (Theoretical Quantiles) và vẽ biểu đồ lợi suất thực tế đã được sắp xếp theo thứ tự tăng dần (Sample Quantiles).
1
2
3
4
from scipy import stats
tq = stats.probplot(r_t)
plt.scatter(x=tq[0][0], y = tq[0][1])
plt.show()
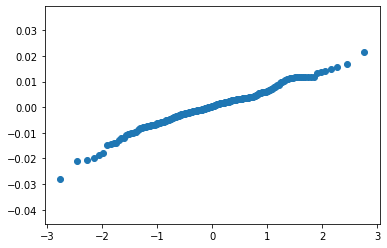
Như vậy từ đồ thị ta có thể khẳng định chuỗi lợi suất có phân phối chuẩn vì đồ thị của phân phối lý thuyết và phân phối thực nghiệm nằm trên cùng một đường thẳng.
3.3. Kiểm tra tính dừng.
Một trong những điều kiện tiền đề khi hồi qui các mô hình chuỗi thời gian đó là chuỗi phải dừng. Để kiểm định tính dừng chúng ta có thể sử dụng kiểm định Argument Dickey Fuller hay còn gọi là kiểm định nghiệm đơn vị. Giả sử ta có một quá trình tự hồi qui $\text{AR}(1)$ đối với chuỗi $y_t$ được xác định như sau: \(y_t = \alpha + \phi y_{t-1} + \epsilon_t\)
Phương trình trên tương ứng với trường hợp chuỗi $y_t$ có hệ số chặn và có xu hướng (tổng quát nhất).
-
Trường hợp chuỗi không có hệ số chặn và có xu hướng: \(y_t = \phi y_{t-1} + \epsilon_t\)
-
Trường hợp chuỗi có hệ số chặn và không có xu hướng: \(y_t = \alpha + \epsilon_t\)
Với $\epsilon_t \sim WN(0, \sigma^2)$ là một chuỗi sai số phân phối nhiễu trắng. Khi khai triển $y_t$ một cách liên tục theo giá trị trễ ta có:
\[\begin{eqnarray} y_t& = & \phi y_{t-1} + \epsilon_t \\ & = & \phi(\phi y_{t-2} + \epsilon_{t-1}) + \epsilon_t \\ & = &\dots \\ & = & \phi(\phi( \dots (\phi y_{0} + \epsilon_{0})+ \dots) + \epsilon_{t-1}) + \epsilon_t \\ & = & \phi^{t}y_0 + \phi^{t-1}\epsilon_{1} + \dots + \phi \epsilon_{t-1} + \epsilon_t \end{eqnarray}\]Do đó
\(\mathbf{E}(y_t) = \phi^{t}\mathbf{E}(y_0)+\mathbf{E}(\phi^{t-1}\epsilon_{1} + \dots + \phi \epsilon_{t-1} + \epsilon_t) = \phi^{t}\mathbf{E}(y_0)\) Dấu bằng thứ 2 xảy ra là do $\text{E}(\epsilon_t)=0,\forall t\in N$ Mặt khác:
\[\begin{equation} \begin{cases} \phi > 1: \lim\limits_{t \rightarrow \infty} \phi^{t} \mathbf{E}(y_0) = \infty \\ \phi = 1: \lim\limits_{t \rightarrow \infty} \phi^{t} \mathbf{E}(y_0) = \mathbf{E}(y_0) \\ \phi < 1: \lim\limits_{t \rightarrow \infty} \phi^{t} \mathbf{E}(y_0) = 0 \end{cases} \end{equation}\]Như vậy tính chất dừng của chuỗi $y_t$ sẽ phụ thuộc vào phương trình đặc trưng $\theta(y)=1−\theta L=0$ có nghiệm đơn vị hay không. Nếu phương trình đặc trưng có nghiệm đơn vị (unit root), chuỗi $y_t$ sẽ không dừng. Trái lại ta có thể khẳng định $y_t$ là chuỗi dừng như đồ thị mô tả bên dưới.

Đồ thị mô tả một khả năng của nghiệm đơn vị. Đường màu đỏ hiển thị sự sụt giảm của output và đường phục hồi nếu chuỗi thời gian có nghiệm đơn vị. Màu xanh hiển thị sự phục hồi nếu không có nghiệm đơn vị và chuỗi là chuỗi dừng có xu hướng (trend-stationary). (Nguồn Unit Root: Simple Definition, Unit Root Tests).
Nhắc lại lý thuyết về kiểm định. Một kiểm định thống kê sẽ bao gồm 2 cặp giả thuyết kiểm định đó là:
-
Gỉa thuyết null (null hypothesis), còn được gọi là
giả thuyết không có, kí hiệu là $H_0$. Đây là giả thuyết bị nghi ngờ xảy ra và được sử dụng để kiểm chứng những tính chất liên quan đến mẫu mà chúng ta chưa biết rằng mẫu sở hữu trên thực tế. Lấy ví dụ, một giáo viên nói rằng các học sinh của trường thi đạt học đạt điểm toán trung bình là 7. Tuy nhiên đây mới chỉ là một giả thuyết cần kiểm chứng. Chúng ta có thể kiểm tra bằng cách thu thập 30 mẫu các học sinh của trường và kiểm chứng giả thuyết của cô giáo bằng cách kiểm định xem trung bình điểm thi toán của 30 học sinh trên có bằng 7 hay không? -
Gỉa thuyết alternative (alternative hypothesis), kí hiệu là $H_1$. Là
giả thuyết thay thếhoặcgiả thuyết đốicó ý nghĩa trái ngược với khẳng định ở giả thuyết null.
Để kiếm tra phương trình đặc trưng của chuỗi có nghiệm đơn vị hay không chúng ta sử dụng kiểm định ADF. Giả thuyết null được đặt ra đó là phương trình đặc trưng có nghiệm đơn vị. Trong trường hợp p-value < 0.05 thì ta sẽ loại bỏ giả thuyết null, chấp nhận giả thuyết thay thế. Khi đó ta có thể khẳng định rằng chuỗi không có nghiệm đơn vị và có tính chất dừng.
\[\begin{equation} \begin{cases} H_0: \phi = 1, \Rightarrow \text{unit root, non-stationary} \\ H_1: |\phi| < 1, \Rightarrow \text{non-unit root, stationary} \end{cases} \end{equation}\]Giá trị ngưỡng kiểm định:
\(DF = \frac{\hat\phi - 1}{SE(\hat\phi)}\)
Chúng ta sẽ so sánh giá trị ngưỡng kiểm định này với giá trị tới hạn của phân phối Dickey - Fuller để đưa ra kết luận về chấp nhận hoặc bác bỏ giả thuyết $H_0$. Trên python đã hỗ trợ kiểm định ADF thông qua package statsmodels. Ta sẽ kiểm định ADF cho chuỗi lợi suất.
1
2
3
4
5
6
7
from statsmodels.tsa.stattools import adfuller
result = adfuller(r_t)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
print('\t%s: %.3f' % (key, value))
1
2
3
4
5
6
ADF Statistic: -14.707253
p-value: 0.000000
Critical Values:
1%: -3.459
5%: -2.874
10%: -2.573
Gía trị p-value < 0.05, kết luận chúng ta sẽ bác bỏ giả thuyết $H_0$. Phương trình đặc trưng không có nghiệm đơn vị. Do đó chuỗi lợi suất có tính chất dừng.
4. Xây dựng mô hình
Ở mục 2.1. ta đã trình bày về mặt lý thuyết của mô hình ARIMA đã khá đầy đủ. Tuy nhiên lý thuyết chỉ là lý thuyết. Chúng ta sẽ phải biến lý thuyết thành thực tiễn thông qua việc thực hành. Phần này chúng ta sẽ cùng thử nghiệm xây dựng một mô hình ARIMA trên python sử dụng dữ liệu được lấy từ package vnquant.
Mục tiêu của mô hình là dự báo lợi suất theo ngày của chuỗi VnIndex 30 từ dữ liệu được khai thác trong giai đoạn từ 02/01/2019 đến 09/12/2019 theo phương pháp ARIMA. Đầu tiên cần phải lựa chọn bậc phù hợp cho mô hình ARIMA.
4.1. Lựa chọn tham số ARIMA(p, d, q)
Tự tương quan (ACF - AutoCorrelation Function): Tự tương quan là một khái niệm quan trọng trong chuỗi thời gian. Hầu hết các chuỗi thời gian sẽ có sự tương quan với giá trị trễ của nó và các giá trị càng gần nhau thì tương quan càng mạnh hoặc các giá trị cùng thuộc 1 chu kì của chuỗi thì sẽ có tương quan cao (chẳng hạn như cùng tháng trong chu kì năm hay cùng quí trong chu kì năm). Chính vì vậy hệ số này mới có tên là tự tương quan. Hệ số tự tương quan được viết tắt là ACF và thường dùng để tìm ra độ trễ của quá trình trung bình trượt $\text{MV}(q)$ để xây dựng các mô hình như ARIMA, GARCH, ARIMAX,… và kiểm tra yếu tố mùa vụ. Hệ số tự tương quan bậc $s$ được xác định như sau:
\[\rho(s,t) = \frac{cov(x_s,x_t)}{\sqrt{\sigma_s\sigma_t}}\]giá trị $\rho(s,t)$ đo lường khả năng dự báo của biến $x_t$ nếu chỉ sử dụng biến $x_s$. Trong trường hợp 2 đại lượng có tương quan hoàn hảo tức $\rho(s,t)=±1$ ta có thể biểu diễn $x_t=\beta_0+\beta_1 x_s$. Hệ số của $\beta_1$ sẽ ảnh hưởng lên chiều của hệ số tương quan. Theo đó $\rho(s, t)=1$ khi $\beta_1>0$ và $\rho(s,t)=−1$ khi $\beta_1<0$. Chúng ta có thể vẽ biểu đồ các hệ số tự tương quan ACF theo các bậc liên tiếp thông qua hàm plot_acf của statsmodels như bên dưới:
1
2
3
4
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
plt.figure(figsize = (8, 6))
ax1 = plot_acf(r_t)
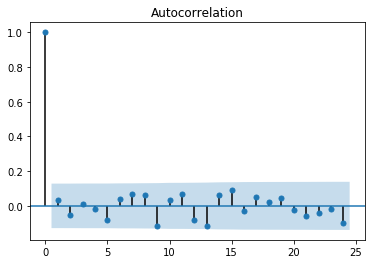
Trục hoành là độ trễ, trục tung là giá trị của hệ số tự tương quan tương ứng với độ trễ. Dải màu hồng chính là khoảng tin cậy 95% để giá trị hệ số tự tương quan bằng 0. Nếu tại một độ trễ nhỏ nhất mà đoạn thẳng (vuông góc với trục hoành) mà độ dài đại diện cho giá trị của hệ số tự tương quan nằm ngoài khoảng tin cậy thì đó chính là độ trễ phù hợp lớn nhất mà ta nên lựa chọn cho quá trình trung bình trượt $\text{MV}(q)$. Nhìn chung bậc $q$ không nên quá lớn. Thông thường tôi chỉ chọn tối đa là 5. Đối với bài toán này toàn bộ các hệ số tự tương quan với bậc nhỏ hơn hoặc bằng 5 đều có giá trị nằm trong khoảng tin cậy 95% của 0. Do đó chúng ta có thể linh hoạt lựa chọn bậc $q=5$ là vị trí mà hệ số tự tương quan lớn nhất.
Tự tương quan riêng phần (PACF - Partitial AutoCorrelation Function): Về cơ bản tương quan riêng phần cũng là chỉ số đo lường hệ số tương quan như ACF. Tuy nhiên vẫn có sự khác biệt đó là hệ số tương quan này loại bỏ ảnh hưởng của các chuỗi độ trễ trung gian (là các chuỗi trễ $x_{t-1}, \dots, x_{t-k+1}$ nằm giữa $x_{t}$ và $x_{t-k}$). Một phương trình hồi qui tuyến tính giữa chuỗi hiện tại với các chuỗi độ trễ trung gian được xây dựng nhằm đánh giá ảnh hưởng của các chuỗi độ trễ lên chuỗi hiện tại. Sau đó, để tính hệ số tương quan riêng phần chúng ta sẽ loại bỏ ảnh hưởng của các độ trễ trung gian khỏi chuỗi hiện tại bằng cách trừ đi giá trị ước lượng từ phương trình hồi qui. Lấy ví dụ: Để tính tự tương quan riêng phần PACF bậc $k$ của chuỗi $x_t$. Đầu tiên ta sẽ hồi qui tuyến tính $x_t$ theo các chuỗi trễ của nó là $x_{t-1},\dots,x_{t-k}$. Khi đó ta thu được phương trình hồi qui tuyến tính tổng quát bậc $k$ là:
\[x_t = \epsilon_t + \alpha_0 + \alpha_1 x_{t-1} + \dots + \alpha_k x_{t-k}\]$\epsilon_t$ là thành phần đại diện cho sai số. Gía trị ước lượng của mô hình đối với $x_t$ chính là:
\[P_{t, k}(x_t) = \alpha_0 + \alpha_1 x_{t-1} + \dots + \alpha_k x_{t-k}\]Hệ số tự tương quan tuyến tính sau đó sẽ chính bằng:
\[\phi_{k} = corr(x_t-P_{t,k}(x_t), x_{t-k}-P_{t,k}(x_{t-k}))\]Trong đó $corr()$ là hàm tính hệ số tương quan. Đó là tất cả về PACF. Khá dễ hiểu phải không nào? PACF sẽ có tác dụng tìm ra hệ số bậc tự do $p$ của quá trình tự hồi qui $\text{AR}(p)$. Tương tự như ACF, thông qua một biểu đồ PACF về giá trị các hệ số tương quan riêng phần tương ứng với các độ trễ khác nhau, chúng ta sẽ tìm ra được các bậc tự do $p$ phù hợp. Đó chính là vị trí mà giá trị của hệ số tương quan riêng phần nằm ngoài ngưỡng tin cậy 95% của giả thuyết hệ số tương quan riêng phần bằng 0.
1
2
3
4
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
plt.figure(figsize = (8, 6))
ax2 = plot_pacf(r_t)
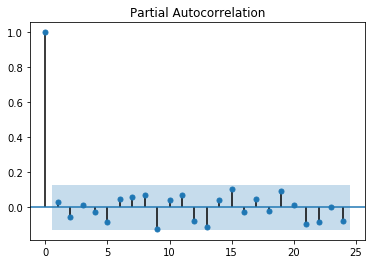
Tương tự như ACF, bậc của PACF cũng thường nhỏ hơn 5. Như vậy ta cũng có thể lựa chọn bậc tự do của PACF là một giá trị nào đó từ 1 đến 5. Kết hợp giữa bậc của $p$ và $q$ và giá trị của $d = 0$ do chuỗi $r_t$ đã là một chuỗi dừng ta có thể thu được một số kịch bản
- ARIMA(2, 0, 2)
- ARIMA(2, 0, 0)
- ARIMA(5, 0, 0)
- ARIMA(0, 0, 5)
4.2. Chỉ số AIC - Akaike Information Criteria
Như vậy chúng ta đã thu được 5 kịch bản mô hình khác nhau và cần chọn ra một mô hình phù hợp nhất. Một trong những tiêu chí thường được sử dụng để lựa chọn mô hình đó là chỉ số AIC (Akaike Information Criteria). Tiêu chí thông tin này là một công cụ ước tính lỗi dự báo và do đó đánh giá chất lượng tương đối của các mô hình thống kê trên một tập hợp dữ liệu nhất định. Gỉa sử có một tập hợp các mô hình được xây dựng trên cùng một bộ dữ liệu, AIC ước tính chất lượng của từng mô hình trong mối liên quan đến từng mô hình khác. Do đó, AIC cung cấp một phương tiện để lựa chọn mô hình. AIC được hình thành dựa trên lý thuyết thông tin (information theory). Khi một mô hình thống kê được sử dụng để dự báo, kết quả sẽ gần như không bao giờ chính xác hoàn toàn. Vì vậy một số thông tin sẽ bị mất do không thể dự báo từ mô hình. AIC ước tính lượng thông tin tương đối bị mất bởi một mô hình nhất định: mô hình mất càng ít thông tin thì chất lượng của mô hình đó càng cao. Giả sử rằng chúng ta có một mô hình thống kê tương ứng với một bộ dữ liệu. Gọi $k$ là số lượng tham số ước tính trong mô hình. Đặt $\hat{L}$ là giá trị tối đa của hàm hợp lý (maximum likelihood function) của mô hình. Khi đó, giá trị AIC của mô hình được tính như sau:
\[AIC = 2k-2\ln(\hat{L})\]Tóm lại rằng giá trị của AIC càng nhỏ thì mô hình của chúng ta càng phù hợp.
4.3. Đọc hiểu kết quả một mô hình ARIMA.
Mô hình ARIMA có thể được xây dựng khá dễ dàng trên python thông qua package statsmodels. Điều mà chúng ta cần thực hiện chỉ là khai báo bậc của mô hình ARIMA. Giả sử cần xây dựng một mô hình ARIMA(2, 0, 0) ta thực hiện như sau:
1
2
3
4
5
from statsmodels.tsa.arima_model import ARIMA
model_arima = ARIMA(r_t, order = (2, 0, 2))
model_fit = model_arima.fit()
print(model_fit.summary())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
ARMA Model Results
==============================================================================
Dep. Variable: y No. Observations: 234
Model: ARMA(2, 2) Log Likelihood 826.298
Method: css-mle S.D. of innovations 0.007
Date: Thu, 12 Dec 2019 AIC -1640.596
Time: 03:35:29 BIC -1619.864
Sample: 0 HQIC -1632.237
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0001 0.000 0.284 0.776 -0.001 0.001
ar.L1.y -0.4287 0.013 -32.278 0.000 -0.455 -0.403
ar.L2.y -0.9927 0.008 -117.855 0.000 -1.009 -0.976
ma.L1.y 0.4624 0.030 15.565 0.000 0.404 0.521
ma.L2.y 0.9997 0.109 9.156 0.000 0.786 1.214
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 -0.2159 -0.9802j 1.0037 -0.2845
AR.2 -0.2159 +0.9802j 1.0037 0.2845
MA.1 -0.2313 -0.9731j 1.0002 -0.2871
MA.2 -0.2313 +0.9731j 1.0002 0.2871
-----------------------------------------------------------------------------
Bảng trên chính là summary kết quả từ mô hình ARIMA.
- Cột
coeflà giá trị hệ số ước lượng từ mô hình tương ứng với các biến ở cột bên tay trái. - Cột
std errlà độ lệch chuẩn của hệ số ước lượng. Từ giá trị ước lượng và độ lệch chuẩn ta có thể tính toán ra được khoảng tin cậy. Cận trên và dưới của khoảng tin cậy là các cột[0.025và0.975]. - Cột
zchính là giá trị ngưỡng tới hạn được suy ra từ phân phối chuẩn hóa. Gía trị ngưỡng tới hạn được tính bằng: \(z = \frac{\beta-\mu}{u_{\alpha/2}\sigma}\) với $\beta$ là giá trị ước lượng, $\mu, \sigma$ là các giá trị trung bình, độ lệch chuẩn của hệ số ước lượng. $u_{\alpha/2}$ là mức phân vị 97.5% của phân phối chuẩn hóa. Do ở đây ta đang kiểm định các giá trị $\beta$ bằng 0 nên trung bình được giả định bằng 0. Tức là $\mu=0$. Nhìn chung là ta không cần quan tâm đến cột này lắm bởi cộtP>|z|đã thực hiện chức năng thay thế nó trong việc kiểm định các hệ số ước lượng có ý nghĩa thống kê hay không. - Cột
P>|z|là xác suất để giá trị $P(\mid X\mid > 0 \mid X \sim N(0, \sigma^2))$. Đây chính là giá trị P-value của cặp giả thuyết dấu bằng. Gía trị của P-value < 0.05 sẽ cho thấy hệ số ước lượng lớn hơn 0 là có ý nghĩa thống kê.
Các chỉ số ở góc trên bên phải lần lượt là:
- No. Observations: Số lượng quan sát
- Log Likelihood: Gía trị hàm logarit ước lượng hợp lý tối đa.
- AIC: Chỉ số Akaike Information Criteria
- BIC: Chỉ số Bayesian Information Criteria. Chỉ số này cũng có chức năng đo lường sai số của mô hình như AIC nhưng theo trường phái thống kê suy diễn (statistical inference).
Như vậy xét trên khía cạnh mô hình thống kê thì tất cả các hệ số ước lượng đều có ý nghĩa thống kê với mức ý nghĩa 95% ngoại trừ giá trị ước lượng của hệ số tự do. Ta có thể thấy các mô hình trong thống kê và kinh tế lượng tuy đơn giản (chỉ là hồi qui tuyến tính) nhưng rất chú trọng tới các yếu tố như:
- Ý nghĩa thống kê của các hệ số ước lượng: Các hệ số ước lượng phải có ý nghĩa thống kê để tác động của các biến phụ thuộc (hoặc biến đầu vào) lên biến độc lập (biến mục tiêu) có thể diễn giải được. Ý nghĩa thống kê ở mức tin cậy 95% có thể được kết luận thông qua so sánh giá trị P-value với 0.05. Nếu giá P-value < 0.05 ta có thể tin rằng 95% giá trị của hệ số ước lượng là khác 0 và biến độc lập tác động lên biến phục thuộc và trái lại.
- Tính giải thích của các hệ số: Trong kinh tế lượng hầu hết các mô hình hồi qui là lớp các mô hình tham số. Tức là tác động của biến phụ thuộc lên biến độc lập thường được giải thích qua một phương trình $y=f(x)$ rất tường minh. Sự tường mình này mang lại nhiều thuận lợi trong việc đánh giá tác động giữa các nhân tố vi mô, vĩ mô lên nhân tố được dự báo.
- Tác động biên: Khoảng tin cậy của tác động biên khá được quan tâm trong các mô hình. Chẳng hạn trong một mô hình về dự báo GDP, thay đổi yếu tố đầu vào là lãi suất thị trường 1% sẽ ảnh hưởng đến GDP như thế nào? Sẽ được giải thích qua một khoảng tin cậy 95% của hệ số ước lượng tương ứng với lãi suất. Đây cũng là một trong những thông tin mà các nhà điều hành, làm chính sách rất quan tâm.
- Mô hình nhân quả: Thường các chuỗi kinh tế vi mô, vĩ mô sẽ có mối quan hệ nhân quả. Nếu một yếu tố là nhân tố tác động làm thay đổi yếu tố khác thì rất có khả năng sự thay đổi đó tác động ngược trở lại làm thay đổi yếu tố ban đầu. Do đó chúng ta thường sẽ có những hệ phương trình nhân quả mà mỗi phương trình con là một phương trình hồi qui của một biến nằm trong hệ nhân quả.
Trên đây là những điểm sơ đẳng nhất mà tôi rút ra từ kinh nghiệm của mình. Ngoài ra còn rất nhiều những sự khác biệt nữa giữa machine learning và thống kê, kinh tế lượng mà làm nhiều chúng ta sẽ tự đúc kết ra. Quay trở lại việc lựa chọn mô hình tốt nhất trong lớp các mô hình ARIMA, đơn giản chúng ta có thể căn cứ trên AIC như sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
from statsmodels.tsa.arima_model import ARIMA
def _arima_fit(orders, data):
models = dict()
for order in orders:
model = ARIMA(data, order = order).fit()
model_name = 'ARIMA({},{},{})'.format(order[0], order[1], order[2])
print('{} --> AIC={}; BIC={}'.format(model_name, model.aic, model.bic))
models[model_name] = model
return models
orders = [(2, 0, 2), (2, 0, 0), (5, 0, 0), (0, 0, 5)]
models = _arima_fit(orders, r_t)
1
2
3
4
ARIMA(2,0,2) --> AIC=-1640.5962884691016; BIC=-1619.8643617769553
ARIMA(2,0,0) --> AIC=-1637.2904778611642; BIC=-1623.4691933997333
ARIMA(5,0,0) --> AIC=-1633.0803506362663; BIC=-1608.8931028287625
ARIMA(0,0,5) --> AIC=-1633.0818121578536; BIC=-1608.8945643503498
Ta nhận thấy mô hình ARIMA(2,0,2) là phù hợp nhất với bộ dữ liệu lợi suất vì nó tương ứng với chỉ số AIC là nhỏ nhất.
4.4. Phương pháp Auto ARIMA
Chúng ta thấy rằng việc lựa chọn mô hình tốt nhất chỉ đơn thuần dựa trên chỉ số AIC, khá đơn giản. Do đó chúng ta hoàn toàn có thể tự động thực hiện qui trình này. Trên python đã hỗ trợ tìm kiếm mô hình ARIMA phù hợp thông qua package auto arima. Chúng hoạt động như một grid search mà tham số chúng ta truyền vào chỉ là các hệ số giới hạn trên của các bậc $(p, d, q)$. Mọi việc còn lại hãy để thuật toán tự giải quyết. Nếu bạn làm quen với R thì cũng hỗ trợ chức năng auto ARIMA tương tự như vậy. Để sử dụng phương pháp auto arima chúng ta phải dùng tới package pyramid. Cài đặt pyramid như bên dưới:
` pip install pyramid-arima `
Xây dựng phương trình hồi qui theo phương pháp Auto ARIMA
1
2
3
4
5
6
7
8
9
10
from pyramid.arima import auto_arima
model = auto_arima(r_t, start_p=0, start_q=0,
max_p=5, max_q=5, m=12,
start_P=0, seasonal=False,
d=0, D=0, trace=True,
error_action='ignore',
suppress_warnings=True,
stepwise=True)
print(model.aic())
1
2
3
4
5
6
Fit ARIMA: order=(0, 0, 0); AIC=-1640.286, BIC=-1633.376, Fit time=0.015 seconds
Fit ARIMA: order=(1, 0, 0); AIC=-1638.538, BIC=-1628.172, Fit time=0.035 seconds
Fit ARIMA: order=(0, 0, 1); AIC=-1638.569, BIC=-1628.203, Fit time=0.042 seconds
Fit ARIMA: order=(1, 0, 1); AIC=nan, BIC=nan, Fit time=nan seconds
Total fit time: 0.119 seconds
-1640.286473393612
Ở đây chúng ta sẽ khai báo điểm bắt đầu và kết thúc của $p, q$, bậc của $d$ và phương pháp điều chỉnh mô hình là stepwise.
Chiến lược stepwise: Là một chiến lược được sử dụng khá phổ biến trong việc lựa chọn biến cho mô hình hồi qui. Chiến lược này sẽ trải qua nhiều bước. Mỗi một bước tìm cách thêm vào hoặc bớt đi một biến giải thích nhằm tạo ra một mô hình mới sao cho sai số giảm so với mô hình gốc. Như vậy càng qua nhiều bước mô hình sẽ càng chuẩn xác hơn và sau khi kết thúc chiến lược ta sẽ thu được một mô hình cuối cùng là mô hình tốt nhất. Tiêu chuẩn để đo lường sai số và ra quyết định lựa chọn thường là AIC.
Trong trường hợp mô hình có yếu tố mùa vụ thì ta sẽ cần thiết lập seasonal = True và kết hợp thêm chu kì của mùa vụ. Chẳng hạn chu kì là 12 tháng thì có thể khai báo D = 12. Khi đó mô hình ARIMA sẽ trở thành mô hình SARIMA (seasonal ARIMA).
Kết quả mô hình tốt nhất thu được là ARIMA(0, 0, 0):
1
model.summary()
| Dep. Variable: | y | No. Observations: | 234 |
|---|---|---|---|
| Model: | ARMA(0, 0) | Log Likelihood | 822.143 |
| Method: | css | S.D. of innovations | 0.007 |
| Date: | Thu, 12 Dec 2019 | AIC | -1640.286 |
| Time: | 04:39:00 | BIC | -1633.376 |
| Sample: | 0 | HQIC | -1637.500 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 0.0001 | 0.000 | 0.255 | 0.799 | -0.001 | 0.001 |
4.5. Kiếm tra yếu tố mùa vụ
Trong một số chuỗi thời gian thường xuất hiện yếu tố mùa vụ. Việc tìm ra chu kì và qui luật mùa vụ sẽ giúp cho mô hình dự báo chuẩn xác hơn. Yếu tố mùa vụ cũng không phải là một trong những yếu tố quá khó nhận biết. Chúng ta có thể dễ dàng phát hiện ra chúng thông qua đồ thị của chuỗi. Chẳng hạn bên dưới là dữ liệu sản xuất công nghiệp điện và khí đốt tại Hoa Kỳ từ năm 1985 đến năm 2019, với tần suất theo tháng. Chúng ta hãy cùng xem biểu diễn đồ thị của chuỗi.
1
2
3
4
5
6
7
import pandas as pd
import matplotlib.pyplot as plt
df_season = pd.read_csv('USAElectricAndGas.csv', parse_dates=['DATE'], index_col='DATE')
df_season.columns = ['Quantity']
print('data frame shape: ', df_season.shape)
df_season.plot(figsize=(16, 4))
1
data frame shape: (418, 1)
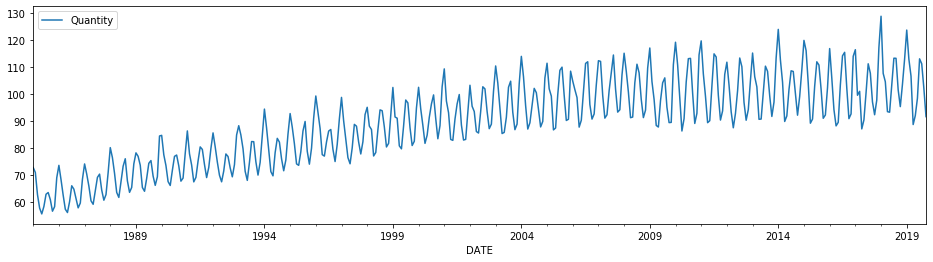
Ta nhận thấy chuỗi có chu kì là 1 năm. Nhu cầu tiêu thụ điện và gas tăng vào những tháng mùa đông do nhu cầu sưởi ấm tăng cao. Ngoài ra chúng ta có thể sử dụng một phép phân rã mùa vụ (seasonal decompose) để trích lọc ra các thành phần cấu thành nên chuỗi bao gồm: xu hướng (trend), mùa vụ (seasonal), phần dư (residual) như bên dưới:
1
2
3
4
from statsmodels.tsa.seasonal import seasonal_decompose
result = seasonal_decompose(df_season, model='multiplicative')
fig = result.plot()
fig.set_size_inches(16, 12)
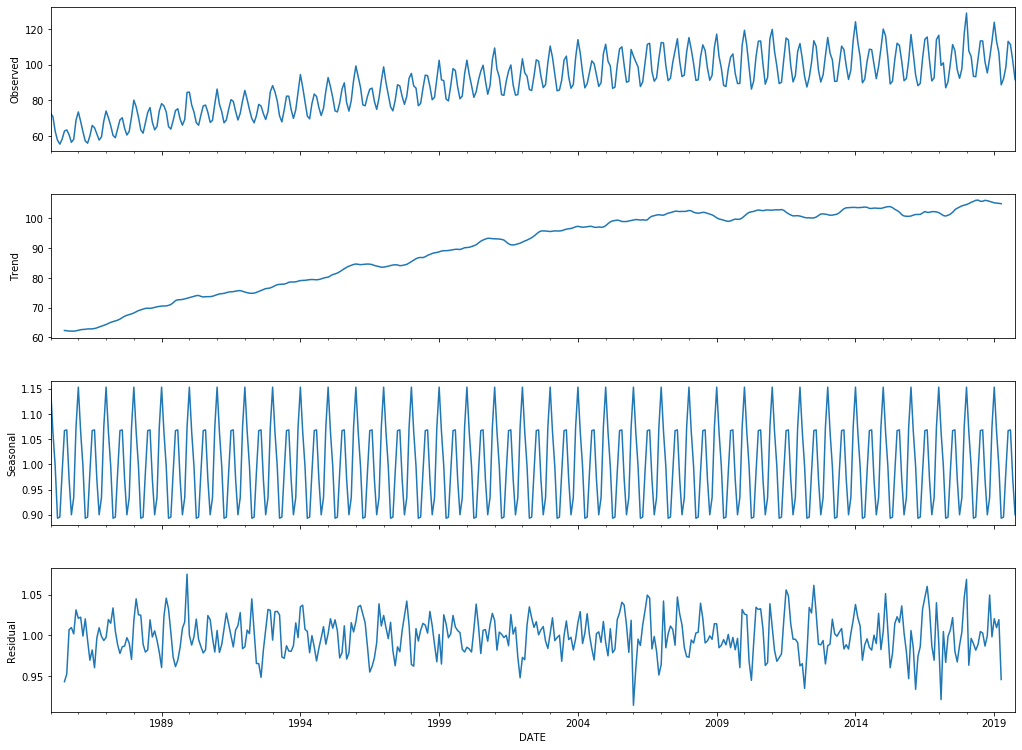
Như vậy các thành phần đã được tách ra khá rõ ràng như thể hiện trong biểu đồ trên. Tiếp theo ta sẽ cùng hồi qui mô hình SARIMA.
4.6. Hồi qui mô hình SARIMA
Phân chia tập train/test Đầu tiên để thuận tiện cho việc kiêm định mô hình dự báo chúng ta sẽ phân chia tập train/test sao cho năm 2019 sẽ được sử dụng làm dữ liệu test và dữ liệu còn lại được sử dụng để huấn luyện mô hình.
1
2
3
train, test = df_season[df_season.index < '2019-01-01'], df_season[df_season.index >= '2019-01-01']
print('train shape: ', train.shape)
print('test shape: ', test.shape)
1
2
train shape: (408, 1)
test shape: (10, 1)
Chúng ta sẽ cùng kiểm tra xem các đặc tính tự tương quan và tương quan riêng phần của chuỗi tiêu thụ điện và gas ra sao. Từ đó quyết định xem quá trình tự hồi qui và trung bình trượt của mô hình ARIMA nên nằm trong khoảng giá trị bao nhiêu và sử dụng phương pháp stepwise để tìm kiếm mô hình phù hợp nhất.
1
2
3
4
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
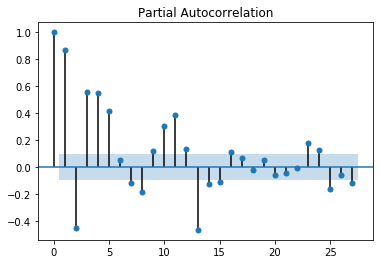
plot_pacf(train)
1
plot_acf(train)
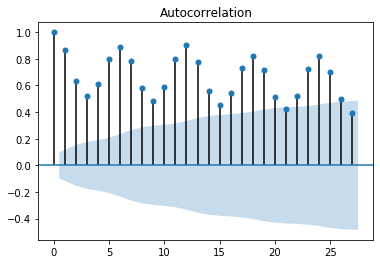
Như vậy từ biểu đồ ta có thể lựa chọn bậc tự tương quan riêng phần PACF và tự tương quan ACF là các giá trị nhỏ hơn hoặc bằng 5. Do chuỗi có trend nên chúng ta sẽ lấy sai phân bậc 1 để tạo chuỗi dừng, hay nói cách khác bậc của intergration $d=1$. Ngoài ra chúng ta cần phải xác định thêm các bậc $(P, D, Q)$ của yếu tố mùa vụ được trích xuất từ chuỗi ban đầu. Để mô hình hiểu được chúng ta đang hồi qui trên mô hình SARIMA thì cần thiết lập tham số seasonal=True và chu kì của mùa vụ m=12. Chiến lược stepwise sẽ tự động tìm cho ta một mô hình tốt nhất dựa trên tham số đã thiết lập.
1
2
3
4
5
6
7
8
9
10
from pyramid.arima import auto_arima
model_sarima = auto_arima(train, start_p=0, start_q=0,
max_p=5, max_q=5, m=12,
start_P=0, seasonal=True,
d=1, D=1, trace=True,
error_action='ignore',
suppress_warnings=True,
stepwise=True)
print(model_sarima.aic())
1
2
3
4
5
6
7
Fit ARIMA: order=(0, 1, 0) seasonal_order=(0, 1, 1, 12); AIC=1944.015, BIC=1955.951, Fit time=0.761 seconds
Fit ARIMA: order=(0, 1, 0) seasonal_order=(0, 1, 0, 12); AIC=2081.725, BIC=2089.682, Fit time=0.050 seconds
...
Fit ARIMA: order=(1, 1, 1) seasonal_order=(2, 1, 2, 12); AIC=1832.589, BIC=1864.420, Fit time=16.458 seconds
Fit ARIMA: order=(2, 1, 2) seasonal_order=(2, 1, 2, 12); AIC=1837.042, BIC=1876.831, Fit time=18.368 seconds
Total fit time: 186.823 seconds
1832.5893833106343
Phương pháp stepwise đã giúp chúng ta tìm được mô hình SARIMA tốt nhất cho bài toán dự báo như bên dưới:
1
model_sarima.summary()
| Dep. Variable: | y | No. Observations: | 408 |
|---|---|---|---|
| Model: | SARIMAX(1, 1, 1)x(2, 1, 2, 12) | Log Likelihood | -908.295 |
| Date: | Thu, 12 Dec 2019 | AIC | 1832.589 |
| Time: | 09:21:50 | BIC | 1864.420 |
| Sample: | 0 | HQIC | 1845.201 |
| - 408 | |||
| Covariance Type: | opg |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| intercept | -0.0022 | 0.001 | -2.509 | 0.012 | -0.004 | -0.000 |
| ar.L1 | 0.5137 | 0.041 | 12.601 | 0.000 | 0.434 | 0.594 |
| ma.L1 | -0.9769 | 0.013 | -76.118 | 0.000 | -1.002 | -0.952 |
| ar.S.L12 | 0.5542 | 0.128 | 4.319 | 0.000 | 0.303 | 0.806 |
| ar.S.L24 | -0.3529 | 0.053 | -6.663 | 0.000 | -0.457 | -0.249 |
| ma.S.L12 | -1.2539 | 0.131 | -9.593 | 0.000 | -1.510 | -0.998 |
| ma.S.L24 | 0.5087 | 0.106 | 4.790 | 0.000 | 0.301 | 0.717 |
| sigma2 | 5.5948 | 0.346 | 16.155 | 0.000 | 4.916 | 6.274 |
| Ljung-Box (Q): | 46.03 | Jarque-Bera (JB): | 12.84 |
|---|---|---|---|
| Prob(Q): | 0.24 | Prob(JB): | 0.00 |
| Heteroskedasticity (H): | 3.05 | Skew: | -0.02 |
| Prob(H) (two-sided): | 0.00 | Kurtosis: | 3.88 |
Warnings:
Đó chính là mô hình SARIMA(p=1, d=1, q=1)(p=2, D=1, q=2, m=12). Mô hình cho kết quả khá tốt khi các hệ số hồi qui đều có ý nghĩa thống kê (toàn bộ cột P>|z| đều nhỏ hơn 0.05).
4.7. Dự báo
Sau khi đã tìm ra được mô hình ARIMA tốt nhất. Chúng ta sẽ dự báo cho khoảng thời gian tiếp theo. Dự báo cho chuỗi thời gian khá đặc thù và khác biệt so với các lớp mô hình dự báo khác vì giá trị time step liền trước sẽ được sử dụng để dự báo cho time step liền sau. Do đó đòi hỏi phải có một vòng lặp liên tiếp dự báo qua các bước thời gian. Rất may mắn là hàm predict() đã tự động giúp ta thực hiện việc đó. Ta sẽ chỉ phải xác định số lượng phiên tiếp theo muốn dự báo là bao nhiêu. Chẳng hạn bên dưới ta sẽ dự báo cho 10 tháng tới tương ứng trên tập test kèm theo giá trị ngưỡng tin cậy của nó.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
n_pred_perious = 10
fitted, confint = model_sarima.predict(n_periods=n_pred_perious, return_conf_int=True)
date = pd.date_range(train.index[-1], periods=n_pred_perious, freq='MS')
fitted_seri = pd.Series(fitted, index=date)
lower = confint[:, 0]
upper = confint[:, 1]
plt.figure(figsize=(12, 6))
plt.plot(df_season[-360:], label='Actual')
plt.plot(fitted_seri, color='red', linestyle='--', label = 'Forecast')
plt.fill_between(date,
lower,
upper,
color='grey', alpha=0.2)
plt.ylim((0, 130))
plt.legend()
plt.title('SARIMA regression model forecast for 12 next months')
plt.show()
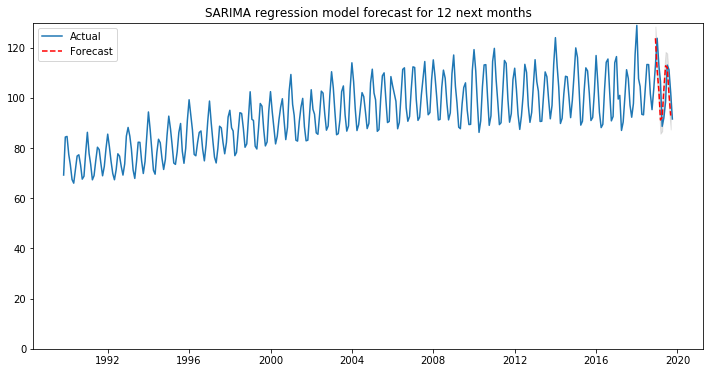
Chúng ta biết rằng một mô hình có thể fit với tập huấn luyện nhưng chưa chắc đã tốt khi dự báo. Chính vì thế cần kiểm tra chất lượng của mô hình trên tập dự báo. Trong mô hình phân loại chúng ta thường quan tâm đến tỷ lệ chính xác accuracy, trong trường hợp mẫu mất cân bằng thì precision, recall, f1 là những chỉ số đo lường độ chính xác khác được thay thế. Tuy nhiên với lớp mô hình dự báo thì sẽ sử dụng một tập hợp các tham số khác liên quan đến đo lường sai số giữa giá trị dự báo và giá trị thực tế. Đó là các chỉ số:
- MSE (mean square error): Trung bình tổng bình phương sai số.
- RMSE (root mean square error): Phương sai hoặc độ lệch chuẩn của chuỗi dự báo so với thực tế.
- MAE (mean absolute error): Trung bình trị tuyệt đối sai số. Chính là khoảng cách theo norm chuẩn bậc 1 giữa giá trị dự báo và giá trị thực tế. Dành cho bạn nếu chưa biết về norm chuẩn bậc 1 hoặc L1 norm.
- MAPE (mean absolute percentage error): Trung bình phần trăm trị tuyệt đối sai số. Chỉ số này cho biết giá trị dự báo sai lệch bao nhiêu phần trăm so với giá trị thực tế. Lưu ý ta chỉ tính được chỉ số này chỉ khi giá trị thực tế đều khác 0.
Các chỉ số này càng nhỏ thì chứng tỏ mô hình dự báo càng khớp với giá trị thực tế. Mô hình có thể được tính toán trên tập test như sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def _measure_metric(y, yhat):
e = y-yhat
mse=np.mean(e**2)
rmse=np.sqrt(mse)
mae=np.mean(np.abs(e))
mape=np.mean(e/y)
print('Mean Square Error: {}'.format(mse))
print('Root Mean Square Error: {}'.format(rmse))
print('Mean Absolute Error: {}'.format(mae))
print('Mean Absolute Percentage Error: {}'.format(mape))
return mse, rmse, mae, mape
mse, rmse, mae, mape=_measure_metric(test.values[0], fitted)
1
2
3
4
Mean Square Error: 476.3896685459648
Root Mean Square Error: 21.826352616641305
Mean Absolute Error: 19.369003668097253
Mean Absolute Percentage Error: 0.1564646147420661
Giải thích ý nghĩa các thông số:
- RMSE: Biên độ giao động của giá trị dự báo xung quanh giá trị thực tế là 21.83.
- MAE: Trung bình sai số giữa giá trị dự báo và giá trị thực tế là 19.37
- MAPE: Sai số giữa giá trị dự báo so với giá trị thực tế bằng 15% giá trị thực tế.
5. Tổng kết
Như vậy tôi đã giới thiệu tới các bạn từ lý thuyết đến thực hành các mô hình ARIMA và SARIMA áp dụng trong các bài toán dự báo chuỗi thời gian. Đây là những lớp mô hình phổ biến và có độ chính xác cao không thua kém gì những mô hình deep learning như LSTM, CNN. Thậm chí một số trường hợp còn cho độ chính xác cao hơn. Tuy nhiên mọi sự so sánh đều chỉ là tương đối, tùy vào bài toán và tùy vào dữ liệu mà chúng ta sẽ cần phải lựa chọn phương pháp phù hợp. Hoặc thậm chí là thử nghiệm nhiều phương pháp khác nhau. Về nội dung của bài viết tôi hi vọng các bạn nắm được:
- Đặc trưng của một mô hình ARIMA thông qua các quá trình tự hồi qui, trung bình trượt và đồng tích hợp.
- Các yêu cầu về tính dừng, tính nhiễu trắng của sai số ngẫu nhiên trước khi thực hiện một mô hình hồi qui ARIMA.
- Tiêu chuẩn và chiến lược lựa chọn các mô hình ARIMA phù hợp với bộ dữ liệu.
- Dự báo và đánh giá kết quả dự báo từ mô hình.
Cuối cùng là phần tài liệu mà tôi đã sử dụng để viết các bài viết này.